The Distribution Properties of Two-Parameter Exponential Distribution Order Statistics
Article Information
Roland Forson1*, Cai Guanghui1, Samuel Ofori2, Oo Than Nweit2, Daniel Ofori Kusi3
1Department of Statistics and Mathematics, Zhejiang Gongshan University, China
2Department of Mathematics and Physics, Zhejiang Normal University, China
3Department of Mathematics, University of Free State, South Africa
*Corresponding Author: Roland Forson, Department of Statistics and Mathematics, Zhejiang Gongshan University, China
Received: 25 April 2019; Accepted: 04May 2019; Published: 10 May 2019
Citation: Roland Forson, Cai Guanghui, Samuel Ofori, Oo Than Nweit, Daniel Ofori Kusi. The Distribution Properties of Two-Parameter Exponential Distribution Order Statistics. Journal of Analytical Techniques and Research 1 (2019): 003-009.
Share at FacebookAbstract
This paper proposes the distribution function and density function of double parameter exponential distribution and discusses some important distribution properties of order statistics. We prove that random variables following the double parameter exponential type distribution X1, X2,..., Xn are not mutually independent and do not follow the same distribution, but that the Xi, Xj meet the dependency of TP2 to establish RTI ( Xi | Xj ), LTD (Xi | Xj ) and RSCI.
Keywords
Order statistics, Double parameter exponential distribution, TP2, RTI, LTD, RSCI
Order statistics articles, Double parameter exponential distribution articles, TP2 articles, RTI articles, LTD articles, RSCI articles
Order statistics articles Order statistics Research articles Order statistics review articles Order statistics PubMed articles Order statistics PubMed Central articles Order statistics 2023 articles Order statistics 2024 articles Order statistics Scopus articles Order statistics impact factor journals Order statistics Scopus journals Order statistics PubMed journals Order statistics medical journals Order statistics free journals Order statistics best journals Order statistics top journals Order statistics free medical journals Order statistics famous journals Order statistics Google Scholar indexed journals Double parameter exponential distribution articles Double parameter exponential distribution Research articles Double parameter exponential distribution review articles Double parameter exponential distribution PubMed articles Double parameter exponential distribution PubMed Central articles Double parameter exponential distribution 2023 articles Double parameter exponential distribution 2024 articles Double parameter exponential distribution Scopus articles Double parameter exponential distribution impact factor journals Double parameter exponential distribution Scopus journals Double parameter exponential distribution PubMed journals Double parameter exponential distribution medical journals Double parameter exponential distribution free journals Double parameter exponential distribution best journals Double parameter exponential distribution top journals Double parameter exponential distribution free medical journals Double parameter exponential distribution famous journals Double parameter exponential distribution Google Scholar indexed journals TP2 articles TP2 Research articles TP2 review articles TP2 PubMed articles TP2 PubMed Central articles TP2 2023 articles TP2 2024 articles TP2 Scopus articles TP2 impact factor journals TP2 Scopus journals TP2 PubMed journals TP2 medical journals TP2 free journals TP2 best journals TP2 top journals TP2 free medical journals TP2 famous journals TP2 Google Scholar indexed journals RTI articles RTI Research articles RTI review articles RTI PubMed articles RTI PubMed Central articles RTI 2023 articles RTI 2024 articles RTI Scopus articles RTI impact factor journals RTI Scopus journals RTI PubMed journals RTI medical journals RTI free journals RTI best journals RTI top journals RTI free medical journals RTI famous journals RTI Google Scholar indexed journals LTD articles LTD Research articles LTD review articles LTD PubMed articles LTD PubMed Central articles LTD 2023 articles LTD 2024 articles LTD Scopus articles LTD impact factor journals LTD Scopus journals LTD PubMed journals LTD medical journals LTD free journals LTD best journals LTD top journals LTD free medical journals LTD famous journals LTD Google Scholar indexed journals RSCI articles RSCI Research articles RSCI review articles RSCI PubMed articles RSCI PubMed Central articles RSCI 2023 articles RSCI 2024 articles RSCI Scopus articles RSCI impact factor journals RSCI Scopus journals RSCI PubMed journals RSCI medical journals RSCI free journals RSCI best journals RSCI top journals RSCI free medical journals RSCI famous journals RSCI Google Scholar indexed journals two-parameter distribution articles two-parameter distribution Research articles two-parameter distribution review articles two-parameter distribution PubMed articles two-parameter distribution PubMed Central articles two-parameter distribution 2023 articles two-parameter distribution 2024 articles two-parameter distribution Scopus articles two-parameter distribution impact factor journals two-parameter distribution Scopus journals two-parameter distribution PubMed journals two-parameter distribution medical journals two-parameter distribution free journals two-parameter distribution best journals two-parameter distribution top journals two-parameter distribution free medical journals two-parameter distribution famous journals two-parameter distribution Google Scholar indexed journals reliability engineering articles reliability engineering Research articles reliability engineering review articles reliability engineering PubMed articles reliability engineering PubMed Central articles reliability engineering 2023 articles reliability engineering 2024 articles reliability engineering Scopus articles reliability engineering impact factor journals reliability engineering Scopus journals reliability engineering PubMed journals reliability engineering medical journals reliability engineering free journals reliability engineering best journals reliability engineering top journals reliability engineering free medical journals reliability engineering famous journals reliability engineering Google Scholar indexed journals two-parameter exponent articles two-parameter exponent Research articles two-parameter exponent review articles two-parameter exponent PubMed articles two-parameter exponent PubMed Central articles two-parameter exponent 2023 articles two-parameter exponent 2024 articles two-parameter exponent Scopus articles two-parameter exponent impact factor journals two-parameter exponent Scopus journals two-parameter exponent PubMed journals two-parameter exponent medical journals two-parameter exponent free journals two-parameter exponent best journals two-parameter exponent top journals two-parameter exponent free medical journals two-parameter exponent famous journals two-parameter exponent Google Scholar indexed journals Sequencial Statistics articles Sequencial Statistics Research articles Sequencial Statistics review articles Sequencial Statistics PubMed articles Sequencial Statistics PubMed Central articles Sequencial Statistics 2023 articles Sequencial Statistics 2024 articles Sequencial Statistics Scopus articles Sequencial Statistics impact factor journals Sequencial Statistics Scopus journals Sequencial Statistics PubMed journals Sequencial Statistics medical journals Sequencial Statistics free journals Sequencial Statistics best journals Sequencial Statistics top journals Sequencial Statistics free medical journals Sequencial Statistics famous journals Sequencial Statistics Google Scholar indexed journals
Article Details
1. Introduction
In this paper, some important properties of order statistics of two-parameter exponential distribution are discussed when the distribution and density functions of a two-parameter distribution is given. We also proved that the random variables X1, X2,..., Xn, obeying the two-parameter exponential distribution are not independent of each other, and do not obey the same distribution. Order statistics is a kind of statistics distribution commonly used in statistical theory and application of which there are many research [1-6]. The two parameter exponential distribution is also a very useful component in reliability engineering. This study considers the nature of order statistics. Its density function and distribution functions are respectively [7];
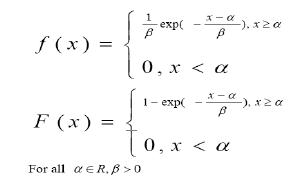
2. Prerequisite Knowledge
2.1 Lemma 1
Let all X follow a continuous distribution function F (x) and its density function of F (x), {a < x < b}, X1, X2,...Xn is a simple random sample with acapacity of N from X2
- The joint probability density function of (X1, X 2,..., X n) if a ≤ X1 < X 2 < ... < Xn ≤ b is

Otherwise,
g1,2,...,n ( X1, X 2, ..., X n ) 0
- The joint probability density function of order statistic (Xi, Xj )(1 ≤ I ≤ j ≤ n) is a ≤ x ≤ y ≤ b and
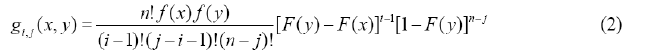
Otherwise,
gi, j (x, y) 0
- The probability density function of order statistics X (k) is
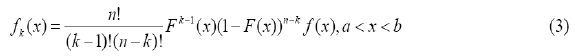
In particular, when k = 1, there is

When k = n, there is

2.2 Lemma 2
Assume that X and Y are two random variables, the joint probability is f (x) if the inequality x1 ≤ x2, y1≤ y2 is satisfied [10].
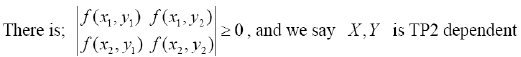
2.3 Lemma 3
For a fixed x, y, if P (X > x, Y > y | X > x1, Y > y1 ) is a monotonic increasing function for variables x1 and y1, then variables X, Y satisfies RSCI [10] .
2.4 Lemma 4
For any y1, if P (Y ≤ y1| X ≤ x1 ) is monotone decreasing function of x1, then Y is the left tail decreasing function of X, denoted by Ltd ( XY ) [11].
2.5 Lemma 5
For any y1, if P (Y > y1 | X > x1 ) is an incremental function of x1, then Y is the right tail growth of X, denoted by RTI (XY) [11].
3. Main Conclusion
3.1 Theorem 1
Let the total X follow a continuous distribution function of F (x) and its density function F (x) (a < x < b), X1, X2,..., Xn be a simple random sample with a capacity of N from the population X, and X1, X2,..., Xn
- The order statistics of the joint probability density function of (X1, X2,..., Xn ) is as follows; a ≤ X1 2 < ... n ≤ b
If then
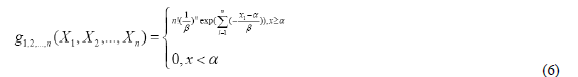
- The probability density function of X k is;
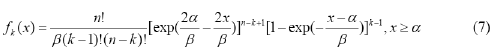
In particular, when k 1, there is

When k= n,
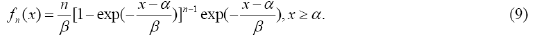
Which is proved from lemma 1.
3.2 Theorem 2
If X1, X2, ..., Xn is independent of each other and obeys a two-parameter exponential distribution, then X1, X2, ..., Xn is not independent of each other and does not obey the same distribution.
Proof : Let n = 2 be used to represent the observations of x1 and x2 with X1 and X2 respectively. It can be seen from lemma 1 that the density function of (X1, X2) is
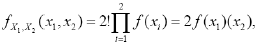
The density functions of X1 and X 2 are respectively
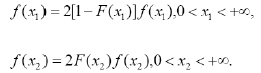
Assuming that X1 and X 2 are independent, then fX1,X 2 (x1, x2 ) = f (x1 ). f (x2 ), and 2 f (x1 ) f (x2 ) = 2[1- F (x1)] f (x1).2F (x2 ) f (x2 ) = 4 [1-F (x1 )]F (x2 ) f (x1 ) f (x2 ).
Therefore,
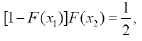
Then,
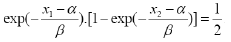
Which obviously does not hold. So
f X1, X 2 (x1, x2 ) ≠ f (x1 ). f (x2)
Therefore, X1 and X 2 are not independent of each other and do not obey the same distribution. Hence proved.
3.3 Theorem 3
If X1, X2,..., Xn are independent of each other and obey the two-parameter exponential distribution, then X i,Yj (I < j) is TP2 dependent.
Proof: The observations of xi and xj are represented by Xi, Xj. For any xi < xj, the joint density function of Lemma 1, is
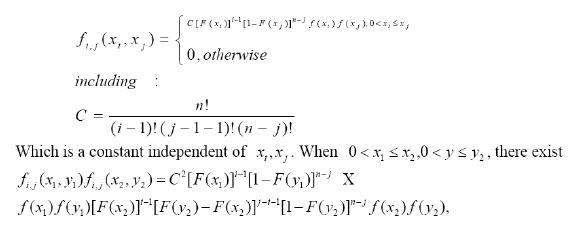
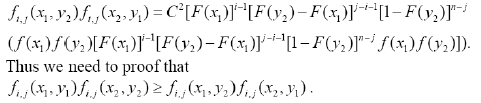
We only need
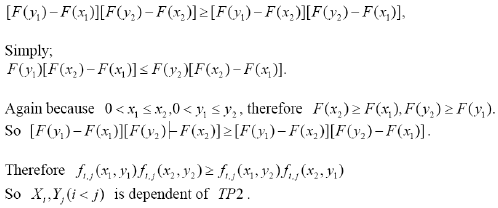
3.4 Theorem 4
Suppose X1, X2, ..., Xn is n independent and identically distributed random variables from the exponential distribution of two parameters, then RTI (Xj | Xi), i< j. It is proved that for any s, t when s > t, there is
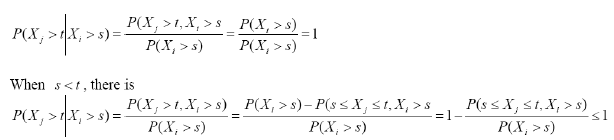
When it is fixed and so increases. The integral of P (≤ Xj ≤ t, Xs) decreases P(s ≤ Xj ≤ t, Xi > s)
P (Xj > t | Xi > s) LTD( Xi | Xj), i < j according to the density functions becomes smaller and becomes larger.
3.5 Theorem 5
Suppose Xi and Xj are two random variables independently obeying the same two-parameter exponent. Then X1 and X2 satisfy RCSI (i.e for fixed X and Y and Y, if P (X x,Y y | X x ', Y y' ) is a monotonic increasing function of variables x' and y', it is proved that the joint density functions of X1 and X2 is f1,2 (x1, x2). When x1, x2 is invariant, P( X1 > x1, X2 > x2 | X1 > x'1, X2 > x'2 ), x'1, x'2 is increasing function

iii When x1 < x'1, x2 > x'2 or x1 > x'x, x2 < x'2 are equally available,
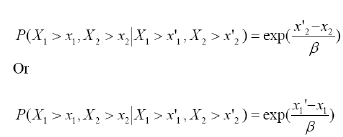
When x1, x2 are fixed, they are incremental functions of x'1, x'2. In conclusion, P( X1 > x1, X2 > x2 | X1 > x'1, X2 > x'2) are incremental functions of x1 ', x'2. So X1, X2 satisfies RSCI.
4. Conclusion
Some distribution properties of order statistics obeying two-parameter exponential distribution are discussed. It is proved that when X1, X2,..., Xn are independent of each other and obey the exponential distribution of two-parameters, the order statistics X1, X2, ..., Xn is not independent of each other and does not obey the same distribution, but Xi, Xj satisfies TP2 dependence. For any i < j, there are RTI ( Xj | Xi ), LTD( Xi | Xj), and X1, X2 that satisfy RSCI.
References
- He Jia, Du Chaoxiong. On the Sequencial Satistical Distribution Properties of Exponential Distribution. Journal of Hunan University of science and technology: Natural science edition 26 (2011): 125-128.
- Jiang Penihua. Distribution properties of Weibull distribution order statistics. Anqing Normal University: NaturalScience Edition 18 (2012): 47-50.
- Kuang Nenghui. The Distribution Properties Two-parameter Rayleigh Distribution Sequencial Statistics. Journal of Jianxi Normal University: Natural Science Edition 33 (2009): 648-651.
- Kuangneng Hui. Distribution Properties of Laplace Distribution Sequence. Journal of Xuzhou Normal University: Natural Science Edition 27 (2009): 34-37.
- Kuangneng Hui. The Distribution properties of Gamma Distribution order statistics. Journal of Lanzhou University of Technology 13 (2010): 17-19.
- Xiong Jiabing, Wang Zhixing. Properties of Uniform Distribution orderStatistics. Advanced mathematics research 13 (2010): 17-19.
- Liu Xuan. Accurate formula for calculating the minimum and maximum moments of ordinal statistics of exponential distribution with two parameters. Journal of Zhengzhou University: Science Edition 47 (2015): 41-44.
- Wang Wei. A Proof of the Distribution Sequential Statistics. Journal of Changchun University 12 (2002): 20-21.
- He Chaobing, Tian Yanwei. Distribution of Sequential Statistics. Journal of Chengdu University.. Natural Science Edition 27 (2008) : 116-119.
- Jin Liqin. Statistical Characteristics of Index Distribution and Geometric distribution. Shanghai: Shanghai Normal University (2013).
- Ave’rous J, Dortet-Bernadet JL. LTD and RTD dependence ordering. Canadian Journal of Statistics 28 (2000): 15-157.
