1. Introduction

The correlation of phenotypes between relatives is the basis for inferring the additive genetic variance underlying the quantitative trait.  Classical methods for inferring genetic variance involves comparisons of variances among relative of known degree.  In natural populations, relatives are largely unknown. We now enter this unknown.

One common measure of population differentiation for a quantitative trait is Q_st.  Wright (1951) showed that  where the total genetic variance is   However, Q_st requires separate estimates of additive genetic variation within populations. One of the greatest limitations of methods for estimating quantitative genetic variance components is the requirement of known relatedness, but molecular marker-based methods for inferring variance components offer the opportunity to overcome this limitation [1].

1.1 Inferring natural quantitative genetic variance

To estimate the additive variance, the main approach is the "squared pair difference" [2].  Let a quantitative trait, such as human height or monkeyflower corolla width, take a numerical value  for individual k at locus i.  This value is the squared difference between the two traits multiplied by the coefficient of relatedness,

The expectation of equation (1) is

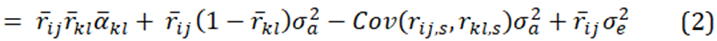
and since population estimates of relatedness have a mean of zero, and the average quantitive gene effect is zero, equation (2) becomes.

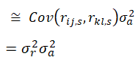
For a total sample size of N pairs, the general estimator is 

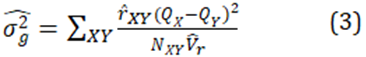
1.2 Estimation of relatedness

To estimate relatedness, there is a choice of many estimators of pairwise relatedness, but with natural, complex population structures, a joint estimation of two- and four-gene relatedness coefficients is warranted, such estimators are given in [1].  A joint estimator can confer reduced bias and variance for either or both coefficients.  At one locus, if individual X has alleles i and j, and individual Y has alleles j and l, the joint estimate of relatedness for that locus is

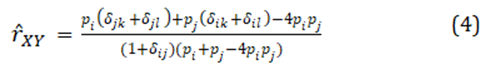
where the indicator variables d are equal to one if the two subscripts have the same numerical value, otherwise they equal zero.  For multilocus estimates, this locus has weight

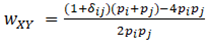
and multilocus estimates are the weighted average over loci.

1.3 Estimation of QST

With adaptive population divergence, directional selection is expected to increase F_ST of selected loci.  The F_ST analogue for a quantitative trait is proportion of additive genetic variance that exists among populations.  The total genetic variance, in the denominator, consists of within- and between- population components, and within-population component is the nemisis of Q_ST which normally requires outside estimates of heritability. 

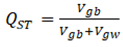
where  and  denote the additive quantitative genetic variances, between and within populations, respectively.   is calculated from a quantiative genetic breeding design, and   is estimated as the among-population variances of mean trait values. 

However, precise Qst estimates are poor [3].  Classical studies of Q_st suffer from a number of biases of estimation. [4]. Ideally, individuals should all be raised in a common garden, but then questions about environmental interactions and phenotypic plasticity arise.  Natural selection alters Qst due to differential survival in the common garden, when the phenotype is correlated with survival such as plant size. The presence of dominance genetic variance causes estimates of parent offspring correlations to be biased upwards, hence the additive genetic variance component of Qst is overestimated.  The joint estimation of two and four gene components of quantitative genetic variance using markers may obviate this problem.

The data is arranged as  and the paired differences fall into to classes.

2. Discussion

The correlation of relationship between loci allows prediction of relatedness at quantitative trait loci based on relatedness at marker loci, and hence allows estimation of heritability [5]. This inference relies on the presence of variation of relatedness among pairs, i.e., some pairs are full sibs, some half-sibs, some unrelated, etc.  At the population level, longer term pedigree relationships enter.  This variation results in a correlation of relatedness between marker and quantitative trait loci, and is the critical factor to quantify for the estimation of heritability.

Both types of estimation use what was originally termed "gene-identity disequilibrium" by Weir and Cockerham (1969). This type of association can be confused with linkage disequilibrium because both have similar genetic effects. For example, apparent overdominance can be caused by linkage disequilibrium between allozyme alleles and deleterious alleles, or by identity disequilibrium between allozyme loci and heterotic loci.  Populations with high identity disequilibrium (consanguineous or bottlenecked populations) could be propitious for using marker-based animal models, but are also more likely to deviate from the standard assumptions of quantitative genetics models (non-additive variance) [6].

Across pairs of individuals i and j, we seek the additive genetic variation , where E denotes the expectation over all individuals X.  Thus in this simplest approach we consider pairs of individuals to estimate variances.  First consider the general case of two individuals sampled at random, irrespective of population origin.  Different pairs of individuals should have different stength of relatedness, as this is a critical component of estimating quantitative genetic variance with neutral genetic markers.  However, we note that if we have a second individual Y with phenotype Q_Y, the product itself Q_XQ_Y cannot estimate genetic variance, correlations between relatives are needed. 

2.1 Using wild populations

Estimates of "heritability in the field" have been few in the literature.  Reviewing empirical and simulation studies of quantitative genetics in wild populations using marker-based estimates of relatedness confirms that it is extremely difficult to derive reliable estimates for quantitative genetic parameters in wild populations using Ritland’s pairwise regression model, as suggested by several authors [26], [65], [66].  However, the loss in rigor from abandoning artificial experiments is offset by the gain in realism, as the genetic components of characters in the field are estimated entirely free of artificial manipulation.

Because one uses natural levels of gene identity and relationship, one has very little choice over "efficient" experimental designs. One cannot design natural populations with a specified, optimal pattern of relationships. The options available are (1) to increase sample size, either through more loci or (preferably) through more individuals, (2) to choose Mendelian loci with greater polymorphism, and (3) to choose species and populations with moderate levels of inbreeding and/or relatedness (and with maximal potential for variation of inbreeding and/or relationship). The third option can introduce a type of bias, as only species that are nonclonal, show limited dispersal, and have local genetic differentiation can be used. For example, to estimate the viability of selfing, species must show natural selfing rates of at least 10%.

Also, the power of estimators of relatedness is limited by the numbers of independent loci so that increasing the number of markers does not necessarily increase statistical power.  Alternative ways to increase power were suggested by [7]: (i) first selecting small subsets of independent and maximally informative markers to be used in relatedness estimation or (ii) using pedigree reconstruction methods to build a relationship matrix based on relationships implied by the reconstructed pedigree.

One approach to get around this problem is to estimate and approximation for Q_ST, termed "P_ST", as proposed by Leinonen et al 2006: 

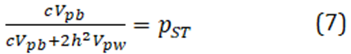
where the subscript p denotes the phenotypic variances, and where h² is the heritability and c is a proportion of additive phenotypic variance among populations ).  However, possible values of Q_ST depend on a range of both h² and c, and required educate guesses about both, or at least heritability measured in the artificial environment. 

Utilization of the information from entire pedigrees in wild populations can be used for superior estimats to those based upon pairwise comparisons [8].

2.2 “Onomics era” data

The availability of genome-wide dense sets of molecular markers (Slate et al. 2009) has made possible heritability estimation in wild populations with varying levels of unknown relatedness between the sampled individuals (e.g. Kruuk 2004; Frentiu et al. 2008; Kruuk & Hill 2008; Pember-ton 2008; Van Raden 2008).  These approaches may suffer from small sibships and incomplete sampling (Wang 2004).   Subtle features of population structure which is weak but detectable with genome scale datasets.  Analysis with traditional marker sets, on the order of dozens of markers, does not give the power to detect weak levels of variation, and in particular, variation of relatedness.

Recent reports of substantial heritability for gene expression and new estimation methods using marker data highlight the relevance of heritability in the genomics era [9]. The use of high-density genetic marker technologies allows novel estimation methods of heritability, for example, estimation in unpedigreed populations and estimation within families, which are free of assumptions about variation between families.

2.3 Model problems

Ritland (1996) defined "phenotypic similarity" of two individuals X and Y where the means are first subtracted off from both from X and Y.  This definition works fine for estimates of heritability within populations and requires that the expected means are same as for X and Y, as we assume both drawn from same population.  Technically the problem arises when

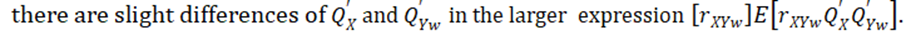
This approach seems to be loosely related to the gene mapping method of [10], which is also based on pairs of observations and the regression of pairwise estimates of phenotypic similarity. Although the effect of shared environment can be included, the limitation of this approach is, in contrast with our main approaches, that it does not allow inclusion of individual-level covariates.  [11] (e.g. year of measurement, hatching data or nest of rearing) into the model (Frentiu et al. 2008) because Ritland’s model is built on pairs of observations.  Despite performing slightly better than the Ritland method, the relationship classes method requires a known family structure with only two classes of relatedness and is therefore of restricted use [6]. 

The most similar approach here is the use of the sharing of human height in relation to exact identity at SNP loci.  For natural populations with complex (but known) pedigrees the "animal model" has been developed to estimate heritability.  The program GCTA for genome-wide complex trait analysis does estimate genetic variance explained by SNPs in an arbitrary population. However, SNPs must be directly associated and not indirectly as in our current approach.  In such approaches, if relatedness coefficients are used to estimate quantitative genetic parameters in association studies, the variance of relatedness needs to be incorporated.

References

1. Lynch M, and K Ritland. Estimation of Pairwise Relatedness with Molecular Markers. Genet 152 (1999): 1753-1766.
2. Grimes L, and W Harvey. Estimation of genetic variances and covariances using symmetric differences squared. J Animal Sci 50 (1980): 634-644.
3. O'Hara RB, and J Merila. Bias and precision in QST estimates: problems and some solutions. Genet 171 (2005): 1331-1339.
4. Whitlock MC. Evolutionary inference from QST. Mol Ecol 17 (2008): 1885-1896.
5. Ritland K. A marker-based method for inferences about quantitative inheritance in natural populations. Evol 50 (1996): 1062-1073.
6. Gay L, M Siol and J Ronfort. Pedigree-Free Estimates of Heritability in the Wild: Promising Prospects for Selfing Populations. PLOS ONE 8 (2013): e66983.
7. Santure AW, J Stapley, A D Ball, et al. On the use of large marker panels to estimate inbreeding and relatedness: empirical and simulation studies of a pedigreed zebra finch population typed at 771 SNPs. Mol Ecol 19 (2010): 1439-1451.
8. Pemberton J M. Wild pedigrees: the way forward. Proceedings of the Royal Society B: Biol Sci 275 (2018): 613-621.
9. Visscher PM, WG Hill and N R Wray. Heritability in the genomics era — concepts and misconceptions. Nat Rev Genet 9 (2008): 255.
10. Haseman JK, and R C Elston. The investigation of linkage between a quantitative trait and a marker locus. Behavior Genet 2 (1972): 3-19.
11. Frentiu Francesca D M, Clegg Sonya J, Chittock T, et al. Pedigree-free animal models: the relatedness matrix reloaded. Proceedings of the Royal Society B: Biol Sci 275 (2008): 639-647.