Introduction

An experiment called CASP (Critical Assessment of Structure Prediction [1]), which has been running since 1996 (in two-year cycles), provides an opportunity to assess progress in the field of protein structure prediction based on amino acid sequence. Participants in this competition propose 3D structures - referred to as models - for an amino acid sequence selected from a list of targets (target - a protein with a native structure known to the organisers). To date, this project has not fully answered questions about the mechanism of the protein folding process [2-19]. The ab initio models (models that are not referenced to available structures in the PDB database) currently used are based on the search for an energy minimum using molecular dynamics simulations [20-24]. A method that has recently made significant progress based on artificial intelligence (AI) techniques provides satisfactory results but with certain limitations [25-27]. In fact, numerous models obtained by known computer programs provided in CASP13 with a level of > 90 on the GDT_TS scale (Global Distance Test - Total Score) are accompanied by examples with a low score [28]. Combining the efforts of the leading teams in the WeFold project provided results with a comparable level of correctness for each team separately [29]. The question relates to the reasons for failure when using software with a high degree of correctness in the other models provided. The simplest answer to this question is that if the model used works very well in some cases and fails in others, it means that the proteins differ in the mechanism by which they have been folded. According to the observations obtained with the FOD-M model, the reason for this lies in the varying environmental conditions, which, by actively participating in the folding process, direct its course in a manner specific to that environment. The high degree of structural heterogeneity is clearly a result of the diversity of amino acid sequences. However, a second factor influencing the variation of the folding process is environmental manipulation. In the polar water environment, an adaptation in the form of exposure of hydrophilic residues on the surface with isolation of hydrophobic residues in the centre of the molecule is evident. In a hydrophobic membrane environment, an exposure of hydrophobic residues on the surface with polar residues in the centre is expected (especially in the case of transmembrane ion channels). These two extreme examples of radical change in the specificity of the local environment suggest the presence of a whole spectrum of changes in the level of polarity of the environment with intermediate characteristics.

In the model discussed in this paper, the structure obtained by simulated folding in an environment conducive to the generation of a micelle-like structure (hydrophobic core at the centre of the protein molecule with exposure of polar residues) is analysed against the native structure, which represents a system with a diffuse distribution of hydrophobicity. The two structural forms, while differing, reveal adjustment to different external conditions. The example discussed here allows us to propose a funnel model that takes into account the factor influencing the selection of an appropriate minimum in a multiple minima problem [30].  The main point of the analysis presented here is to introduce the environmental factor (external force field) as a factor that directs the folding process in a manner specific to that environment. Comparison of the structure obtained for polar water environment conditions with the native structure that functions in a periplasmic environment reveals structural differences. The discussed chain folding in a water environment is not able to obtain a native structure, which features a significantly different external environment. 

Materials and Methods

Data

The two structures of the lactococcin 972 protein from Lactococcus lactis subsp. Lactis. One structure is the 2LGN available in PDB ID ID [31]. The other is a model obtained using the UNRES program with an additional module directing the in silico folding process towards the generation of a hydrophobic core and the exposure of polar residues on the surface. In this procedure, optimisation of energy is accompanied by optimisation of the ordering of hydrophobicity towards a micelle-like distribution. A detailed description is provided in [32].

Model applied

A model called fuzzy oil drop in its modified version of FOD-M [33] was used to describe both structures. The model assumes that polypeptide chains made up of bipolar molecules - amino acids - during the folding process in a polar water environment tend towards a micelle-like structure. This means aiming for a concentration of hydrophobic residues in the centre of the molecule with exposure of polar residues on the surface. Such a hydrophobicity distribution can be described by a 3D Gaussian function spanned over the body of the protein:

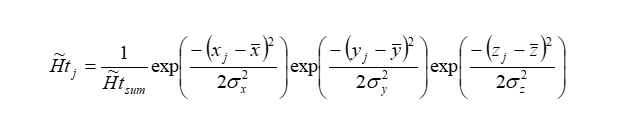
The size and shape of the protein is expressed by the adjusted values of the σ_X, σ_Y and σ_Z parameters, respectively. The theoretical hydrophobicity level determined for a given effective atom calculated using eq. 1 is denoted hereafter as T_i.

The actual distribution may vary, as expressed by the function determining an inter-amino acid interaction. Such interaction depends on the distance between the effective atoms (the averaged position of the atoms comprising a given amino acid) [34]:

Where r_ij - distance between the positions of the effective atoms and c - cutoff distance adopted from [34] 9 Å. H^r means intrinsic hydrophobicity - any scale may be applied [35]. The observed hydrophobicity level determined for a given effective atom calculated using eq. 2 is denoted hereafter as O_i.

Both distributions after normalisation can be subjected to comparative analysis using Kullback-Leibler divergence entropy [36].

Where the tested distribution P (in the model used here - distribution O), distribution Q - the reference distribution (in the model used here - distribution O). 

The value of DKL thus determined cannot be interpreted. Therefore, a second reference distribution R with values R_i=1/N is introduced, where N is the number of amino acids in the polypeptide chain is introduced. Such a distribution is opposite to the T distribution (hydrophobic core), representing a uniform distribution throughout the protein body.

The two values describing the status of a protein can be replaced by a single RD (relative distance) parameter:

A value of RD < 0.5 indicates "proximity" of the O distribution to the T distribution and thus denotes a protein with a hydrophobic nucleus present. RD > 0.5 indicates structuring without the presence of a hydrophobic nucleus.

The aqueous environment is not the only one in which proteins exhibit biological activity. The membrane environment requires reverse distribution in the form of exposure of hydrophobic residues on the surface with a polar centre (mainly for ion channels). In this situation, the function describes the expected distribution of hydrophobicity.

However, it appears that the hydrophobicity distributions identified in membrane proteins show a distribution expressed as the following function:

Where T_i denotes the distribution expressed by the 3D Gaussian function modified by the presence of the function T_MAX - T_i to the extent expressed by the parameter K.

Proteins with K=0.0 (distribution compliant with the distribution expressed by the 3D Gaussian function) and K < 0.4 are down-hill, fast-folding and ultra-fast-folding, including type II antifreeze proteins [37]. The vast majority of domains treated as individual structural units show a structure described by low RD and K values [38]. In contrast, membrane proteins show values in the range of 0.9 < K < 3 [39].

A graphical representation of the model in question (FOD-M) is visualised in Figure1.

Figure 1: Graphical representation of the discussed model (FOD-M) reduced to a one-dimensional example.

A-  idealised distribution (Gaussian function) - T - blue line, observed distribution O - pink line, distribution R - grey line.

B- the RD value determined for the set of distributions as shown in A is 0.702.

C- the value of the K parameter determined for the minimum value of D_KL(O|M) designated for the set of profiles shown in A is 0.5.

D- a compilation of the distributions T (blue), O (pink) and M (cyan) for the designated optimum K.

The value of K is determined as that value of this parameter for which D_KL(O|M) takes a minimum (Fig. 1B). This procedure provides the form of the modified T distribution (M distribution) closest to the O distribution.

Protein status is determined by two parameters:

1. RD - this value indicates the extent to which the micelle-like hydrophobicity distribution is reproduced.
2. K - the value of this parameter determines the specificity of the environment directing the folding process reproducing the presence of the hydrophobic nucleus.

The program used is UNRES, which comes with a micelle-like environment introduction module. The UNRES (UNited RESidues) program is a significant tool in the field of protein structure prediction. A detailed presentation of this program is given in [24, 29, 32].

Results

The analysis presented here aims to propose a model for in silico protein folding that takes into account the diverse environment.

The status of the structures in question: a native protein and a model for an identical amino acid sequence obtained using the in silico method is presented in Tab. 1. The structure of the model was obtained by means of a procedure which, in addition to optimising the internal energy, also includes a procedure which directs the folding towards the generation of a hydrophobic (micelle-like) nucleus [32].

Table 1: Parameters expressing the status of the discussed structures: RD and K - parameters describing the hydrophobicity distribution in protein, parameters σ_X, σ_Y and σ_Z, express the size and shape of molecule (3D Gauss function parameters) .

A compilation of parameter values (Tab. 1) identifies the model as a globular protein with a near spherical shape (3D Gaussian function parameters comparable). The status of the model clearly indicates the presence of a centric hydrophobic nucleus. A low K parameter value indicates shaping directed by the polar environment. The parameter values for the native structure reveal its elongated shape (Sigma parameter values varied). A high RD value indicates a distribution that is rather close to uniform (R distribution). A relatively high K value indicates the proportion of the environment with a significant presence of a hydrophobic agent.

Figure 2: Characteristics of the structures discussed.

A - set of T, O and M profiles for the value of K=0.6 together with a 3D presentation of the native structure of this protein.

B -T (blue), O (red) and M (green) profiles for the value of K=0.2 together with a 3D presentation of the model structure determined for this protein.

Axis in A and B:  vertical - hydrophobicity, horizontal - residues according to sequence.

The comparison of the T, O and M profiles for the native protein suggests significant differences between the T distribution and the O distribution. The optimally fitted M distribution also reveals significant differences to the T distribution.

The high agreement of the T, O and M distributions with a low K value highlights the micelle-like organisation of hydrophobicity in the native form. It is also evident that the globular form of the resulting model is clearly visible, in contrast to the native form showing significant elongation (Sigma parameter values quantify this Table 1.).

The data presented in Tab. 1 allows the results obtained to be presented using the funnel model. The model visualises the multiple minima problem in relation to the energy states. The modification of the funnel model introduced using the FOD-M model is to introduce a quantitative assessment of the factor expressed by the horizontal axis (X-axis). In the visualisations of the model presented so far, the funnel is qualitative in character. In the visualisations of the funnel model to date, the horizontal axis is not described or is limited to qualitative concepts. According to the FOD-M model used, it simply expresses the value of the K parameter, i.e. the variability of the environment preferring different structuring (Figure 2).

Figure 3: Funnel model applied to the protein lactococcin 972 from Lactococcus lactis: comparison of native structure and a structural model for this protein. Model is folded incorrectly.

In order to complement and expand the model examples, the status of the structures proposed for the T0953s2-D3 target have been summarised.

Using the interpretation based on the FOD-M model, the status of the individual models can be interpreted. A funnel model could also be proposed for this set, taking into account the value of the K parameter on the horizontal axis, which would indicate the contribution of external factors to the process of “folding” the models discussed. The force fields applied to obtain the forms in question can be interpreted as a force field tailored to the conditions expressed by the value of the K parameter. 

In the presentation of Fig. S1, revealing the status of the models as expressed by the values of the RD and K parameters, specific groups with common characteristics are distinguished:

1. The navy blue pentagon in Fig. S1 represents the values of the parameters describing the status of the protein acting as a target (Fig. S2-A).
2. The red oval indicates structures with low RD and K values - structures that could theoretically be obtained in an aqueous environment acting as a factor that directs the folding process towards the micelle-like arrangement.
3. The light blue oval is distinguished by K values for structures with a local distribution mismatch against the micelle-like arrangement. Elimination of residues showing mismatch allows the identification of a micelle-like part. Such structures are obtained by means of folding in a water environment, where the amino acid sequence does not allow the micelle-like form to be fully reconstituted.
4. The dark blue oval indicates structures that could be obtained under conditions where a chaperone or chaperonin is present.
5. Spot highlighted by dark blue square - largely unfolded structure (Fig. S2B).

On the vertical axis in the funnel model, there is energy value. Here, the value of the RD parameter, which can also be interpreted as a sort of energy state associated with the presence of a hydrophobic core, is given as a factor characterising the status of a given model (model structures indicated by the red oval in Fig. S1). The presence of a hydrophobic core, together with the possible presence of disulphide bonds, is regarded as a factor stabilising the tertiary structure of proteins. Others, lacking or having a deformed hydrophobic core, can be interpreted as less stable. Energy status is not the only criterion for structural correctness. Structural correctness is the assurance of biological activity, which does not necessarily represent an energy minimum. According to the FOD-M model, a stable structure is one with a low internal energy level but adapted to the conditions directing a given folding process.

It can be speculated that the force fields used by the participants providing models for the T0953s2-D3 target in CASP13 are parameterised in a specific, different way favouring a particular type of folding.

Figure 4: Summary of the RD and K parameter values for

A- the models provided in the CASP13 project - T0953s2-D3 target. The colour variation classifies the protein structures described in the text - blue pentagon - the status of target protein

B- the real proteins listed in Tab. 2. The blue squares - membrane proteins.

A very interesting point representing extremely high RD and K values is a structural form that is unfolded to a considerable extent (Fig. 4). Theoretically, a structure of this type would have to be in highly altered (in relation to polar water) external conditions preventing the formation of a packed globular form.

Figure 5: 3D structures:

A- T0953s2-D3 target structure

B- model with the highest RD and K values (distinguished in Fig. 3.A by blue square)

Table 2: The set of randomly selected proteins representing the spectrum of K values.

Discussion

The target T0953s2-D3 (CASP13) discussed in detail in [28] is an example of a set of models representing the full spectrum of environmental conditions (a detailed description of these models is given in Supplementary Materials). A protein target characterised by extremely low RD and K values, representing a micelle-like distribution, turned out to be a target far from the typical parameterisation of the numerical techniques used, which in their majority represent parameterisations corresponding to a status with an RD close to 0.6 [28]. This value is probably due to the fact that the techniques for the force field parameterisation used in the applied models are based on the analogy of structures available in databases including the PDB. According to our analyses (unpublished data), most proteins represent such a level on the K parameter scale in their large numbers.

The funnel model shape proposals available in the literature treat structural variation qualitatively, in contrast to the model proposed here, where the distribution of the energy minimum is attributed to the corresponding value of the parameter characterising the environment for the folding process [61-66].

It is assumed that environmental changes leading to amyloid transformation will enable simulation of this transformation by way of gradually changed environmental specificity by introducing stepwise variation of the K parameter considered in the form of external force field record [67]. This type of analysis has been positively validated using the example of membrane proteins, whose specific form of membrane anchoring has been shown to be varied [39].

The mathematical model, which shall be applied for simulation In Silico of folding process is the multi-object optimisation [68]. The energy, the minimum of which is searched shall take into account the dependence on two functions as shown below:

Where: F(r_ij) the function expressing the energy status of protein as dependent on two functions: f_INT (r_ij) - internal force field generating the status dependent on the r_ij distances between interacting atoms according to non-bonding interactions and f_EXT(K, r_ij) - external force field depending also on r_ij distances and on K value modifying the external conditions (eq. 6) which influences the structuralisation process of protein. The two f functions act contradictory. The minimisation f_INT (r_ij) may cause the increase of f_EXT(K, r_ij) values and vice versa. The method called front Pareto is the one specially oriented on finding the solution represented by the consensus between these two functions [69].

Conclusion

The funnel model expressing the multiple minima problem can be solved by introducing conditions imposed by the external force field. Correct models provided for subsequent targets (CASP project) are obtained for those proteins, for which the force field parameterisation (or other evaluation criteria) is consistent with the environmental conditions. Obtaining the correct structure for this protein via the In Silico route definitely requires the varying environmental influences to be taken into account. It should be noted that the protein in question is active in the periplasmic space. This environment - as this example shows - influences structure formation in a different way to the aquatic environment. This is made apparent by the funnel model form limiting the potential for structural variation to a narrow range of the K parameter reflecting the environmental conditions for the folding protein. The innovation proposed in this analysis is to give a quantitative form to the horizontal axis in the funnel model, which in other forms of this model is defined qualitatively. The conclusion regarding simulation In Silico of protein folding process, it is necessary to treat such procedure as multi-object optimisation. The minimised energy expressing the status of protein shall be treated as the function dependent on two functions: internal force field (non-bonding interactions) and external force field (specific influence of environment expressed by K parameter). The consensus for these two functions shall be found for final structure of folded protein.

Acknowledgements

Many thanks to Anna Śmietańska and Zdzisław WiŚniowski for technical support. This research was partially supported by the European Union's Horizon 2020 programme under grant Sano No. 857533. and the Sano project carried out within the International Research Agendas programme of the Foundation for Polish Science, co- financed by the European Union under the European Regional Development Fund.

We gratefully acknowledge Poland's high-performance Infrastructure PLGrid ACK Cyfronet AGH for providing computer facilities and support within computational grant “plgdrippy”.

Author contributions

Conceptualisation: IR, LK; Advisory: IR; Calculation : MS

Funding

This research was funded by Jagiellonian University Medical College grant number N41/DBS/001127.

Data availability

All data can be made available via a request addressed to the corresponding author. The program enabling the calculation of RD is accessible on the GitHub platform: https://github.com/KatarzynaStapor/FODmodel and on the platform https://hphob.sano.science

Data presented in Supplementary Materials are attached to this submission - Excel file with data and profiles for proteins described in Tab. 2.

Declarations

Ethics approval and consent to participate

Neither human nor animal data are used in the presented research.

Consent to publication

Not applicable.

Competing interests

The authors declare no conflict of interest.

References

1. https://predictioncenter.org/ accessed Dec 15, 2023
2. Dill KA, Ozkan SB, Weikl TR, et al. The protein folding problem: when will it be solved? Curr Opin Struct Biol 17 (2007): 342-346.
3. Park H, DiMaio F, Baker D. CASP11 refinement experiments with ROSETTA. Proteins 84 (2016): 314-322.
4. MacCallum JL, Pérez A, Schnieders MJ, et al. Assessment of protein structure refinement in CASP9. Proteins 79 (2011): 74-90.
5. Runthala A. Protein structure prediction: challenging targets for CASP10. J Biomol Struct Dyn 30 (2012): 607-615.
6. Taylor TJ, Bai H, Tai CH, et al. Assessment of CASP10 contact-assisted predictions. Proteins 82 (2014): 84-97.
7. Dill KA, MacCallum JL. The protein-folding problem, 50 years on. Science 338 (2012): 1042-1046.
8. Cheng J, Choe MH, Elofsson A, et al. Estimation of model accuracy in CASP13. Proteins 87 (2019): 1361-1377.
9. Kinch LN, Li W, Monastyrskyy B, et al. Assessment of CASP11 contact-assisted predictions. Proteins 84 (2016): 164-180.
10. Kryshtafovych A, Moult J, Baslé A, et al. Some of the most interesting CASP11 targets through the eyes of their authors. Proteins 84 (2016): 34-50.
11. Kryshtafovych A, Monastyrskyy B, Fidelis K, et al. Evaluation of the template-based modeling in CASP12. Proteins 86 (2018): 321-334.
12. Simpkin AJ, Sánchez Rodríguez F, Mesdaghi S, et al. Evaluation of model refinement in CASP14. Proteins 89(2021 ): 1852-1869.
13. Waterhouse A, Bertoni M, Bienert S, et al. SWISS-MODEL: homology modelling of protein structures and complexes. Nucleic Acids Res 46 (2018): W296-W303.
14. Bitencourt-Ferreira G, de Azevedo WF. Homology modeling of protein targets with MODELLER. Methods Mol Biol 2053 (2019): 231-249.
15. Studer G, Tauriello G, Bienert S, et al. ProMod3-A versatile homology modelling toolbox. PLoS Comput Biol 17 (2021): e1008667.
16. Chivian D, Robertson T, Bonneau R, et al. Ab initio methods. Methods Biochem Anal 44 (2003): 547-557.
17. Wu S, Skolnick J, Zhang Y. Ab initio modeling of small proteins by iterative TASSER simulations. BMC Biol 5 (2007): 17.
18. Hardin C, Pogorelov TV, Luthey-Schulten Z. Ab initio protein structure prediction. Curr Opin Struct Biol 12 (2002): 176-181.
19. Bonneau R, Baker D. Ab initio protein structure prediction: progress and prospects. Annu Rev Biophys Biomol Struct 30 (2001): 173-189.
20. Osguthorpe DJ. Ab initio protein folding. Curr Opin Struct Biol 10 (2000): 146-152.
21. Urbanc B, Borreguero JM, Cruz L, et al. Ab initio discrete molecular dynamics approach to protein folding and aggregation. Methods Enzymol 412 (2006): 314-338.
22. Wang Y, Shi Q, Yang P, et al. Fueling ab initio folding with marine metagenomics enables structure and function predictions of new protein families. Genome Biol 20 (2019): 229.
23. Hardin C, Pogorelov TV, Luthey-Schulten Z. Ab initio protein structure prediction. Curr Opin Struct Biol 12 (2002): 176-181.
24. Liwo A, Khalili M, Scheraga HA. Ab initio simulations of protein-folding pathways by molecular dynamics with the united-residue model of polypeptide chains. Proc Natl Acad Sci USA 102 (2005): 2362-2367.
25. Senior AW, Evans R, Jumper J, et al. Improved protein structure prediction using potentials from deep learning. Nature 577 (2020): 706-710.
26. Quraishi M. AlphaFold at CASP13. Bioinformatics 35 (2019): 4862-4865.
27. Callaway E. Deepmind’s AI predicts structures for a vast trove of proteins. Nature 595 (2021): 635.
28. Roterman I, Stapor K, Konieczny L. Role of environmental specificity in CASP results. BMC Bioinformatics 24 (2023): 425.
29. Khour GA, Liwo A, Khatib F, et al. WeFold: a coopetition for protein structure prediction. Proteins 82 (2014): 1850-1868.
30. Roterman I, Konieczny L. External force field - the specific conditions for protein folding - submitted
31. Turner DL, Lamosa P, Martinez B. Structure and properties of lactococcin 972 from lact lactis. - PDB
32. Roterman I, Sieradzan A, Stapor K, et al. On the need to introduce environmental characteristics in ab initio protein structure prediction using a coarse-grained UNRES force field. J Mol Graph Model 114 (2022): 108166.
33. Roterman I, Konieczny L. Protein Is an Intelligent Micelle. Entropy (Basel) 25 (2023): 850.
34. Levitt MA. A simplified representation of protein conformations for rapid simulation of protein folding. J. Mol. Biol 104 (1976): 59-107.
35. Kalinowska B, Banach M, Konieczny L, et al. Application of Divergence Entropy to Characterize the Structure of the Hydrophobic Core in DNA Interacting Proteins Entropy 17 (2015): 1477-1507.
36. Kullback S, Leibler R. A On information and sufficiency. Annals Mathemat Statistics 22 (1951): 79-86.
37. Banach M, Stapor K, Konieczny L, et al. Downhill, Ultrafast and Fast Folding Proteins Revised. Int J Mol Sci 21 (2020): 7632.
38. Sałapa K, Kalinowska B, Jadczyk T, et al. Measurement of Hydrophobicity Distribution in Proteins - Non-redundant Protein Data Bank. Bio-Algorithms and Med-Systems 8 (2012): 327338.
39. Roterman I, Stapor K, Konieczny L. Transmembrane proteins-Different anchoring systems. Proteins 2023.
40. Patskovsky Y, Romero R, Freeman J, et al. Crystal structure of n-Terminal domain of positive transcription regulator evga from escherichia coli. PDB.
41. Bonanno JB, Freeman J, Bain KT, et al. Crystal structure of putative nudix hydrolase family member from chromobacterium violaceum. PDB.
42. Anger AM, Armache J-P, Berninghausen O, et al. Structures of the human and Drosophila 80S ribosome Nature  497 (2013): 80-85.
43. Joint center for structural genomics (jcsg) Crystal structure of a hypothetical glycoside hydrola (bvu_0247) from bacteroides vulgatus atcc 8482 at 2.4 resolution. PDB
44. Zhang Z, Chamala S, Evans B, et al. The crystal structure of dehydrogenase from sinorhizo meliloti. PDB
45. Mace PD, Wallez Y, Dobaczewska MD, et al.NSP-Cas protein structures reveal a promiscuous interaction module in cell signaling. Nat Struct Mol Biol 18 (2011): 1381-1387.
46. Tang W-K, Wong K-B, Lam Y-M, et al. The crystal structure of seabream antiquitin reveals the structural basis of its substrate specificity. FEBS Lett 582 (2008): 3090-3096.
47. Baradaran R, Berrisford JM, Minhas GS, et al. Crystal structure of the entire respiratory complex I. Nature 494 (2013): 443-448.
48. Naganuma M, Sekine Si, Fukunaga R, et al. Unique protein architecture of alanyl-tRNA synthetase for aminoacylation, editing, and dimerization. Proc Natl Acad Sci USA 106 (2009): 8489-8494.
49. Abrescia NGA, Cockburn JJB, Grimes JM, et al. Insights into assembly from structural analysis of bacteriophage PRD1. Nature 432 (2004): 68-74.
50. Oswald C, Smits SHJ, Höing M, et al. Crystal structures of the choline/acetylcholine substrate-binding protein ChoX from Sinorhizobium meliloti in the liganded and unliganded-closed states. J Biol Chem 283 (2008): 32848-32859.
51. Mikolosko J, Bobyk K, Zgurskaya HI, et al. Conformational flexibility in the multidrug efflux system protein AcrA. Structure 14 (2006): 577-587.
52. Xiayang Qiu X, Anil Mistry A, Mark J Ammirati MJ, et al. Crystal structure of cholesteryl ester transfer protein reveals a long tunnel and four bound lipid molecules. Nat Struct Mol Biol 14 (2007): 106-113.
53. Jones BC, Logsdon NJ, Josephson K, et al. Crystal structure of human cytomegalovirus IL-10 bound to soluble human IL-10R1. Proc Natl Acad Sci U S A 99 (2002): 9404-9409.
54. Evdokimov AG, Mekel M, Hutchings K, et al. Rational protein engineering in action: The first crystal structure of a phenylalanine tRNA synthetase from Staphylococcus haemolyticus. Struct. Biol 162 (2008): 152-169.
55. Krieg S, Huché F, Diederichs K, et al. Heme uptake across the outer membrane as revealed by crystal structures of the receptor-hemophore complex. Proc Natl Acad Sci U S A 106 (2009): 1045-1050.
56. Eren E, Vijayaraghavan J, Liu J, et al. Substrate specificity within a family of outer membrane carboxylate channels. PLoS Biol 10 (2012): e1001242.
57. Jackson LP, Kelly BT, McCoy AJ, et al. A large-scale conformational change couples membrane recruitment to cargo binding in the AP2 clathrin adaptor complex. 2010; 141(7): 1220-1229.
58. Huang Y, Smith BS, Chen LX, et al. Insights into pilus assembly and secretion from the structure and functional characterization of usher PapC. Proc Natl Acad Sci U S A 106 (2009): 7403-7407.
59. Hearn EM, Patel DR, Lepore BW, et al. Transmembrane passage of hydrophobic compounds through a protein channel wall. Nature 458 (2009): 367-370.
60. Zhang R, Hryc CF, Cong Y, et al. 4 Å cryo-EM structure of an enveloped alphavirus Venezuelan equine encephalitis virus. EMBO J 30 (2011): 3854-3863.
61. Finkelstein AV, Bogatyreva NS, Ivankov DN, et al. Protein folding problem: enigma, paradox, solution. Biophys Rev 14 (2022): 1255-1272.
62. Nassar R, Dignon GL, Razban RM, et al. The Protein Folding Problem: The Role of Theory. .J Mol Biol 433 (2021): 167126.
63. Wolynes PG. Evolution, energy landscapes and the paradoxes of protein folding. Biochimie 119 (2015): 218-230.
64. Kapon R, Nevo R, Reich Z. Protein energy landscape roughness. Biochem Soc Trans 36 (2008): 1404-1408.
65. Ivankov DN, Finkelstein AV. Solution of Levinthal's Paradox and a Physical Theory of Protein Folding Times. Biomolecules 10 (2020): 250.
66. Schug A, Onuchic JN. From protein folding to protein function and biomolecular binding by energy landscape theory. Curr Opin Pharmacol 10(2010): 709-714.
67. Roterman I, Stapor K, Fabian P, et al. In Silico Modeling of the Influence of Environment on Amyloid Folding Using FOD-M Model. Int J Mol Sci 22 (2021): 10587.
68. Gunantara N. A review of multi-objective optimization: Methodsand its applications. Cogent Engineering 5 (2018): 1502242.
69. Nanda V, Belure SV, Shir OM. Searching for the Pareto frontier in multi-objective protein design. Biophys Rev 9 (2017): 339-344.