Ensemble Machine Learning to “Boost” Ubiquitination-sites Prediction
Article Information
Xiaoye Mo, Xia Jiang1*
1Department of Biomedical Informatics, University of Pittsburgh, Pittsburgh, PA
*Corresponding author: Xia Jiang. Department of Biomedical Informatics, University of Pittsburgh, Pittsburgh, PA.
Received: 10 February 2023; Accepted: 17 February 2023; Published: 27 February 2023
Citation: Xiaoye Mo, Xia Jiang. Ensemble Machine Learning to “Boost” Ubiquitination-sites Prediction Journal of Bioinformatics and Systems Biology. 6 (2023): 47-59.
Share at FacebookAbstract
Ubiquitination-site prediction is an important task because ubiquitination is a critical regulatory function for many biological processes such as proteasome degradation, DNA repair and transcription, signal transduction, endocytoses, and sorting. However, the highly dynamic and reversible nature of ubiquitination makes it difficult to experimentally identify specific ubiquitination sites. In this paper, we explore the possibility of improving the prediction of ubiquitination sites using ensemble machine learning methods including Random Forest (RF), Adaptive Boosting (ADB), Gradient Boosting (GB), and eXtreme Gradient Boosting (XGB). By doing grid search with the 4 ensemble methods and 6 comparison non-ensemble learning methods including Naïve Base (NB), Logistic Regression (LR), Decision Trees (DT), Support Vector Machine (SVM), LASSO, and k-Nearest Neighbor (KNN), we find that all the four ensemble methods significantly outperform one or more non-ensemble methods included in this study. XGB outperforms 3 out of the 6 nonensemble methods that we included; ADB and RF both outperform 2 of the 6 non-ensemble methods; GB outperforms one non-ensemble method. Comparing the four ensemble methods among themselves. GB performs the worst; XGB and ADB are very comparable in terms of prediction, but ADB beats XGB by far in terms of both the unit model training time and total running time. Both XGB and ADB tend to do better than RF in terms of prediction, but RF has the shortest unit model training time out of the three. In addition, we notice that ADB tends to outperform XGB when dealing with small-scale datasets, and RF can outperform either ADB or XGB when data are less balanced. Interestingly, we find that SVM, LR, and LASSO, three of the non-ensemble methods included, perform comparably with all the ensemble methods. Based on this study, ensemble is a promising way of significantly improving Ubiquitinationsite prediction using protein segment data.
Keywords
Machine learning, Ensemble methods; Adaboosting, XGB, Random Forest, Ubiquitination, Ubiquitination-site, PCP, Protein physicochemical properties, Prediction.
Machine learning articles; Ensemble methods articles; Adaboosting articles; XGB articles; Random Forest articles; Ubiquitination articles; Ubiquitination-site articles; PCP articles; Protein physicochemical properties articles; Prediction articles.
Machine learning articles Machine learning Research articles Machine learning review articles Machine learning PubMed articles Machine learning PubMed Central articles Machine learning 2023 articles Machine learning 2024 articles Machine learning Scopus articles Machine learning impact factor journals Machine learning Scopus journals Machine learning PubMed journals Machine learning medical journals Machine learning free journals Machine learning best journals Machine learning top journals Machine learning free medical journals Machine learning famous journals Machine learning Google Scholar indexed journals Ensemble methods articles Ensemble methods Research articles Ensemble methods review articles Ensemble methods PubMed articles Ensemble methods PubMed Central articles Ensemble methods 2023 articles Ensemble methods 2024 articles Ensemble methods Scopus articles Ensemble methods impact factor journals Ensemble methods Scopus journals Ensemble methods PubMed journals Ensemble methods medical journals Ensemble methods free journals Ensemble methods best journals Ensemble methods top journals Ensemble methods free medical journals Ensemble methods famous journals Ensemble methods Google Scholar indexed journals Adaboosting articles Adaboosting Research articles Adaboosting review articles Adaboosting PubMed articles Adaboosting PubMed Central articles Adaboosting 2023 articles Adaboosting 2024 articles Adaboosting Scopus articles Adaboosting impact factor journals Adaboosting Scopus journals Adaboosting PubMed journals Adaboosting medical journals Adaboosting free journals Adaboosting best journals Adaboosting top journals Adaboosting free medical journals Adaboosting famous journals Adaboosting Google Scholar indexed journals XGB articles XGB Research articles XGB review articles XGB PubMed articles XGB PubMed Central articles XGB 2023 articles XGB 2024 articles XGB Scopus articles XGB impact factor journals XGB Scopus journals XGB PubMed journals XGB medical journals XGB free journals XGB best journals XGB top journals XGB free medical journals XGB famous journals XGB Google Scholar indexed journals Ubiquitination articles Ubiquitination Research articles Ubiquitination review articles Ubiquitination PubMed articles Ubiquitination PubMed Central articles Ubiquitination 2023 articles Ubiquitination 2024 articles Ubiquitination Scopus articles Ubiquitination impact factor journals Ubiquitination Scopus journals Ubiquitination PubMed journals Ubiquitination medical journals Ubiquitination free journals Ubiquitination best journals Ubiquitination top journals Ubiquitination free medical journals Ubiquitination famous journals Ubiquitination Google Scholar indexed journals Ubiquitination-site articles Ubiquitination-site Research articles Ubiquitination-site review articles Ubiquitination-site PubMed articles Ubiquitination-site PubMed Central articles Ubiquitination-site 2023 articles Ubiquitination-site 2024 articles Ubiquitination-site Scopus articles Ubiquitination-site impact factor journals Ubiquitination-site Scopus journals Ubiquitination-site PubMed journals Ubiquitination-site medical journals Ubiquitination-site free journals Ubiquitination-site best journals Ubiquitination-site top journals Ubiquitination-site free medical journals Ubiquitination-site famous journals Ubiquitination-site Google Scholar indexed journals Protein physicochemical properties articles Protein physicochemical properties Research articles Protein physicochemical properties review articles Protein physicochemical properties PubMed articles Protein physicochemical properties PubMed Central articles Protein physicochemical properties 2023 articles Protein physicochemical properties 2024 articles Protein physicochemical properties Scopus articles Protein physicochemical properties impact factor journals Protein physicochemical properties Scopus journals Protein physicochemical properties PubMed journals Protein physicochemical properties medical journals Protein physicochemical properties free journals Protein physicochemical properties best journals Protein physicochemical properties top journals Protein physicochemical properties free medical journals Protein physicochemical properties famous journals Protein physicochemical properties Google Scholar indexed journals Prediction articles Prediction Research articles Prediction review articles Prediction PubMed articles Prediction PubMed Central articles Prediction 2023 articles Prediction 2024 articles Prediction Scopus articles Prediction impact factor journals Prediction Scopus journals Prediction PubMed journals Prediction medical journals Prediction free journals Prediction best journals Prediction top journals Prediction free medical journals Prediction famous journals Prediction Google Scholar indexed journals Random Forest articles Random Forest Research articles Random Forest review articles Random Forest PubMed articles Random Forest PubMed Central articles Random Forest 2023 articles Random Forest 2024 articles Random Forest Scopus articles Random Forest impact factor journals Random Forest Scopus journals Random Forest PubMed journals Random Forest medical journals Random Forest free journals Random Forest best journals Random Forest top journals Random Forest free medical journals Random Forest famous journals Random Forest Google Scholar indexed journals
Article Details
1. Background
Ensemble learning is a technique that learns multiple models from the same dataset and then combines them to form an optimal learner, which is anticipated to have better prediction performance. Supervised learning provides algorithms to perform a searching task with limited hypothesis space to find an optimal hypothesis which will manage the prediction task successfully with a specific problem [1]. However, it can be challenging to find a suitable hypothesis for a particular problem, even when the hypothesis space is well designed. The ensemble method in machine learning, which combines different hypotheses to hopefully construct a much better hypothesis, has been discussed for decades. With multiple models, it can reduce the classification error rate in a classification task [2].
Empirically, ensemble learning is expected to provide better results when a substantial diversity is found among models, which sometimes may cause over-fitting or under-fitting [3,4]. With this experience, researchers tried to develop many ensemble learning methods which could take advantage of the diversity among different models and then combine them together [3,5,6]. Although it may not be intuitive, stochastic algorithms (e.g., random decision trees) could be used to generate stronger ensemble models than intentional algorithms (e.g., entropy-reducing decision trees) [7]. Moreover, using a variety of powerful learning algorithms has already been shown to be more effective than using techniques that try to simplify the model to promote diversity [8].
Although there can be many ways to implement ensemble learning, we focused on two approaches which are widely discussed and applied in practice [9-12]: bootstrap aggregating and boosting. Bootstrap aggregation, also called bagging (from bootstrap aggregating), is usually applied to decision tree methods, but can also be applied to any other method [13,15]. As implied in its name, bootstrap and aggregation are two key components of bagging. Bootstrap is a sampling method. Given a standard training set D of size n, bagging generates m new sub-training sets Di, each of size n', by sampling from D randomly with replacement. By sampling with replacement, some observations may be repeated in each Di, but some observations may not appear in any subset Di. When sampling uniformly, if n'=n, for large n, the set Di is expected to have the fraction (1 - 1/e) (≈63.2%) of the unique examples of the original set D, the rest being duplicates [16]. After the bootstrapped sampling, several sub-datasets are created. Each sub-dataset will be used by a machine learning method to train a model, which will result in multiple models trained using different sub-datasets. Since each bootstrap set is randomly generated, the sets of the sub-datasets are expected to be diversified, and therefore, the individual models in the ensemble are expected to represent a different aspect of the original data. Due to this, when combining all sub-models together, the ensemble is expected to represent aspects of the original data. Finally, the ensemble will make predictions through simple statistics such as voting. Figure 1(a) on the left illustrates the general components and procedures of bagging.
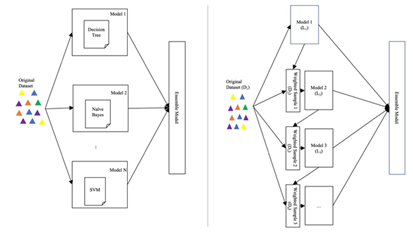
Figure 1: An illustration of Ensemble methods (a) Bagging (b) Boosting.
Boosting is the third main approach of ensemble learning, which involves incrementally building the ensemble and training new model instances by focusing on wrong results made by previous trained models [17-19]. Boosting comes from the famous question from Kearns and Valiant: “Can a set of weak learners create a single strong learner?”[20]. In 1990, Robert offered an answer to that question, which significantly influenced machine learning, and also led to the development of boosting [19]. Later, researchers have proved that boosting can have better accuracy than bagging in some cases, but it may not handle the over-fitting issue as well [21]. Figure 1(b) on the right shows the general idea of boosting: the same weight is given to each training data D1 at the beginning. The base learner L1 will learn Model1 from D1. Then, the wrongly classified instances by Model1 will be given a larger weight than the correct ones. The second base learner L2 will learn Model 2 from the weighted data D2, and so on and so forth. The voting algorithm is applied in the final round to produce the results.
Ubiquitination, also called ubiquitylation is an enzymatic and post-translational modification process in which ubiquitin, a small regulatory protein, is attached to substrate proteins [22,23] During the ubiquitination process, ubiquitin interacts with lysine (K) residues on protein substrates through three steps: ubiquitin-activating enzymes (E1s), ubiquitin-conjugating enzymes (E2s), and ubiquitin ligases (E3s) [22-24]. It needs to be mentioned that binding can be a single ubiquitin or a ubiquitin chain. It has been found that many regulatory functions of ubiquitination, such as proteasome degradation, DNA repair and transcription, signal transduction, endocytosis, and sorting, are important protein regulatory functions in biological processes [22-25].
Because ubiquitination plays an important regulatory role, extensive research has been conducted to further decipher the mechanism of ubiquitination and other regulatory roles at the molecular level. One of the initial and challenging steps in gaining a greater understanding of ubiquitination is to identify ubiquitination sites. To purify ubiquitinated proteins to determine ubiquitination sites, researchers have used different types of experimental methods, such as high-throughput mass spectrometry (MS) techniques [26-29], ubiquitin antibodies and ubiquitin-binding proteins [29,30], and combined liquid chromatography and mass spectrometry [31]. However, experiments to purify ubiquitinated proteins are time-consuming, expensive, and labor-intensive because the ubiquitination process is dynamic, rapid, and reversible [24,32,33]. To reduce experimental costs and increase the effectiveness and efficiency of ubiquitination site identification, computational (in silico) methods based on informatics techniques have been introduced and developed for predicting ubiquitination sites based on prior knowledge of protein sequences [24,25,32,33].
A previous research applied some basic machine learning methods to predict ubiquitination-site with PhysicoChemical Property (PCP) datasets [34]. As we know, a protein is a biological molecule that consists of one or more long chains of amino acid residues; PCP datasets are generated from protein sequences and then are processed by several steps, including segment extraction, creating AA-PCP matrix, and averaging [34]. Although the study demonstrated the potential of conducting this challenging task by taking the machine learning approach, results from the base machine learning methods were not completely satisfactory. Since ensemble methods are proved to do better than base learners in many cases, we conjectured that they are potentially powerful in predicting ubiquitination-sites. In this research, we considered four widely used state of art ensemble methods including Random Forest (RF), Adaptive Boosting (ADB), Gradient Boosting (GB), and eXtreme Gradient Boosting (XGB). To verify our conjecture, we conducted ubiquitination-site prediction by learning prediction models using these methods from previously published PCP datasets [34].
2. Methods
As described above, we did the experiments with two widely used types of ensemble methods, Bagging and Boosting. RF is one of the most famous Bagging approaches of ensemble learning [35]. RF was published in 2001 by Breiman, which utilizes Bagging to generate different subsets for entire training to build individual decision trees [35]. Then, RF has been applied into different fields research, including chemical, power transmission, ecology, etc. [14,36,37]. ADB, GB, and XGB are three Boosting approaches. AdaBoost was purposed by Freund and Schapire around 1996 [18,38]. In 2001, Friedman proposed the GB method, opening the door to Boosting [39]. XGB, a new development based on GB, was proposed by Chen and He in 2005 [40]. Unlike RF, the other three methods are Boosting algorithms, and the main idea of boosting is to build models sequentially based on previous trained models [41].
Since ensemble methods were said to improve the performance of prediction models in many cases, we tried to apply them on the ubiquitination-site prediction task. Hyperparameter tunning with grid search is a state-of-the-art approach to improve prediction performance. In this study, we optimized 4 ensemble learning models by performing hyperparameter tuning via grid search. We next describe the six PCP datasets we used. We will then describe each of the four existing ensemble methods we used, including RF, ADB, GB, and XGB. We will also describe the grid search we conducted, the hyperparameter values we used in the grid search for each of these methods, and the evaluation metrics we used.
2.1 Datasets
The six (PCP) datasets were curated and published in 2016 by Cai and Jiang [34]. As shown in Table 1, each dataset contains 531 features. These 6 datasets can be divided by 2 types. PCP 1-3 are balanced datasets, meaning each dataset contains the same number of positive and negative cases, while PCP 4-6 are imbalanced datasets with unequal numbers of positive and negative cases. Also, PCP 1 and 6 are small-scale datasets with less than a thousand cases each, and PCP 2-5 are large-scale datasets which contain thousands of data points each.
|
Total # of cases |
# Positive cases |
# Negative cases |
# Features |
|
|
PCP-1 |
300 |
150 |
150 |
531 |
|
PCP-2 |
6838 |
3419 |
3419 |
531 |
|
PCP-3 |
12236 |
6118 |
6118 |
531 |
|
PCP-4 |
4608 |
363 |
4345 |
531 |
|
PCP-5 |
3651 |
131 |
3520 |
531 |
|
PCP-6 |
676 |
37 |
639 |
531 |
Table 1: Case counts of the datasets
2.2 Ensemble Methods
Ensemble learning is a combination machine learning method that combines the prediction results from multiple models to have an overall good performance. Among the three most popular types of ensemble learning, there are some shared points. First, ensemble learning models all use individual models to train, which means they combine several trained models, unlike traditional machine learning models which are only trained once. However, all “small” prediction models may use different combinations to build the final ensemble model [42]. Bagging, stacking, and boosting are the three most popular methods of combination. Random Forest is one of the most popular bagging methods [35], AdaBoosting, Gradient Boosting, and Extreme Gradient Boosting are widely used boosting algorithms [39,43,44]. Second, while traditional machine learning methods usually need constraints on a dataset (for example, a balanced dataset), ensemble learning can handle imbalance problems, with a well-designed ensemble model, it can perform well [45]. In this study, we performed ensemble learning with the methods mentioned above, to analyze how they work with ubiquitination-site prediction.
2.3 4 ensemble ML methods
We compared the performance of a set of ensemble machine-learning methods, including Random Forest (RF), Adaptive Boosting (ADB), Gradient Boosting (GB), and eXtreme Gradient Boosting (XGB). Like most machine learning methods, these methods have hyperparameters that can be tuned to provide optimal performance. We conducted a grid search for each method for 6 PCP datasets. We conducted 5-fold cross-validation for each set of hyperparameter values and measured the performance by the AUC of ROC (Receiver Operating Characteristic). Below, we provide a summary of the hyperparameters and their values that we tested for each of these 4 ensemble methods. All the test values are shown in Table 2.
RF [7,11,35,36,46] is a typical model of bagging in ensemble learning, the trainer will randomly select a certain amount of sample data and create corresponding decision trees to form a random forest [11]. An advantage of random forest is that the independent character of each decision tree tends to reduce overfitting [36,46]. n_estimators: The number of decision trees in the random forest. We tested values 10, 50, 100, 200, 300. The parameter max_depth indicates how deep the tree can be; the deeper the tree, the more splits it will have, and thus capturing more information about the data [7,11,35]. We fit a decision tree with depths ranging from 2 to 32. The parameter min samples split represents the minimum number of samples required to split an internal node. The values we tested in our grid search were 0.1, 0.2, 0.3, 0.4, 0.6, 0.8, 0.9 and 1. Max features indicated the maximum number of features allowed when building a decision tree [46,49,50]; we tested all values under ‘none’, ‘log2’ and ‘sqrt’. The parameter max leaf nodes controls the maximum number of leaf nodes of each decision tree [7,11,35], and we tested values 7, 10, 15, and none. The parameters max depth and max leaf nodes are important in controlling overfitting [36]. The function criterion was used to measure the quality of a split [7,11,35]; We tested with values ‘gini’ and ‘entropy’.
ADB [11,18,35,47,48] is a typical model of boosting in ensemble learning [11,35]. Unlike the random forest model, where each decision tree is independent, Adaboost is a classifier with a cascade structure, which means the next learner is based on the result of the previous weak learner [18,35]. During the learning process, if the current sample is classified incorrectly, the degree of difficulty of the sample will increase to make the next learner focus on the difficult part on which the previous model performed poorly [47,48]. N estimators: The number of weak learners. A model to overfit for large values of n estimators; The values of n estimators we tested include 10, 20,…, 100, 200, and 300. Learning rate: this is used to shrink the contribution of each classifier; We tested values include 0.002, 0.003, 0.004, …, 0.01, and 0.02.
|
Method |
Hyperparameter Name |
Values |
|
RF |
n_estimators |
10, 50, 100, 200, 300 |
|
var_smoothing |
10-9, 10-8, 10-7, …, 10-1 |
|
|
criterion |
gini, entropy |
|
|
splitter |
best, random |
|
|
max_depth |
2, 4, 6, …, 32 |
|
|
max_features |
auto, sqrt, log2 |
|
|
min_samples_split |
0.1, 0.2, 0.3, …, 1.0 |
|
|
min_samples_leaf |
1 |
|
|
max_leaf_nodes |
7, 10, 15, None |
|
|
class_weight |
None, balanced |
|
|
ADB |
algorithm |
SAMME, SAMME.R |
|
n_estimators |
[10, 20, 30, …, 100, 200, 300] |
|
|
learning_rate |
[0.002, 0.003, 0.004, …, 0.01, 0.02] |
|
|
GB |
criterion |
frideman_mse, mse |
|
learning_rate |
[0.01, 0.1, 0.3] |
|
|
n_estimators |
[50, 100, 150] |
|
|
max_depth |
[3, 6, 9] |
|
|
XGB |
gamma |
[0,0.01,0.1] |
|
learning_rate |
[0.01,0.1,0.3] |
|
|
n_estimators |
[50, 100, 150] |
|
|
max_depth |
[3,6,9] |
|
|
reg_alpha |
[1e-3,1e-2,0.1] |
|
|
reg_lambda |
[1e-3,1e-2,0.1] |
Table 2: Machine learning hyperparameters and values
GB [39,41,49-52] is an ensemble of weak predictions models [39]. Unlike the bagging methods, boosting builds the mode in sequentially [52]. Boosting fits base learners additively to have better performance than random [41,50,51]. Learning rate, one of the most important hyper-parameters, we tested 0.01, 0.1, 0.3. The number of boosting stages to perform, n estimator, we tried 50, 100, and 150 to test. The values of max depth we tested include 3, 6, and 9. criterion which is a function to measure the split, and here we tested two different criterions, ‘friedman mse’ and ‘mse’.
XGB [40,43,52,53] is another common approach for boosting in ensemble learning. Unlike ADB, it uses gradient boosting [52]. The XGB classifier is based on the difference between true and predicted values to improve model performance [40,53]. gamma: this is a pseudo-regularization hyperparameter in gradient boosting; gamma affects pruning to control overfitting problems. gamma values we tested were 0, 0.01, and 0.1. alpha and lambda are both regularization hyperparameters which can help control overfitting [40]. The values we tested for each of them were 1e-3, 1e-2, and 1e-1. max depth is the maximum depth of the individual regression estimators. The values of max depth we tested were 3, 6, and 9. The learning_rate values we tested were 0, 0.01, 0.1, and 0.3.
2.4 Grid Search
Machine learning algorithms have been widely used in different types of tasks in the real world. To have the machine learning math perform well in a specific task, it often needs a tuning procedure with which we can find a good set of hyperparameters values [54], which we call a hypermeter setting. There are many ways to perform hyper-parameter searching, such as grid search, random search, and manual search [55]. Grid search is a systematic way of finding the best hyperparameter setting by training models using all possible settings automatically, which are determined by the preselected ranges of values of the hyperparameters. In this study, we incorporated grid search into our program by using the grid search procedure provided in the scikit-learn Python package [56]. We conducted grid search for all ensemble learning methods and all comparison methods included in this study.
With researchers devoting, grid search has been approved in various fields, as it has been found to improve the machine learning prediction model performance, such as the prediction of HIV/AIDS [57], text classification [58], and short-term PV power forecasting [37]. In this research, we proved that grid search can also improve the performance of ensemble learning in ubiquitination-site prediction tasks.
2.5 Performance metrics, 5-fold cross-validation, and statistical testing
We performed grid search and recorded 64 different output values for each of the models trained, organized using an output format that we designed. Contained within the output data is information about the computer system used, computation time, and measures for model performance. For a given binary diagnostic test, a receiver operator characteristic (ROC) curve plots the true positive rate against the false positive rate for all possible cutoff values [59]. The area under curve (AUC) measures the discrimination performance of a model. We conducted 5-fold cross-validation to train and evaluate each model in a grid search. The entire dataset was split into a train-validation set, containing 80 percent of the cases, and an independent test set, containing the remaining 20 percent. We then performed a 5-fold cross validation by dividing evenly the train-validation set into 5 portions. The division was mostly done randomly except that each portion had approximately 20% of the positive cases and 20% of the negative cases to ensure that it was a representative fraction of the dataset. Training and testing were repeated five times. Each time, a unique portion was used as the validation set to test the model learned from the training set, which combined the remaining four portions. Training and testing AUCs were reported. The average training and testing AUC over all five times were also derived and reported. The best-performing set of hyperparameter values was chosen based on the highest mean test AUC. The best model would be the one refitted from the entire train-validation set using the best-performing set of hyperparameters values. We used this procedure for all methods.
We conducted statistical testing to further evaluate the prediction performance of the ensemble methods. We did both two-sided and one-sided tests. Wilcoxon rank-sum tests to rank the 4 ensemble methods in terms of their prediction performance. We also compared the ensemble methods with traditional machine learning methods, again using both two-sided and one-sided Wilcoxon rank-sum tests. With the two-sided testing, we try to determine whether there is a significant difference between the comparison methods in terms of their prediction performance, and if there is, we then try to determine which method is better with the one-sided test.
3. Results
We compared the prediction performance of the best models which were selected by grid search in different aspects. The results are shown in Table 3-8 and Figure 2-5. Table 3 shows the side-by-side comparisons of the validation AUCs of the best performing models of all four ensemble methods for each of the six PCP datasets. Also included in Table 3 are the average and maximum validation AUCs for each method over all datasets and for each dataset over all methods. Based on Table 3, on average of all datasets, the ranking of the four ensemble methods is as follows: XGB (1st, AUC 0.721), ADB (2nd, 0.720), RF (3rd, 0.706), and GB (4th, 0.689). Table 4 contains the running time information and number of models trained via grid search in this study. The hyperparameters settings for the best models identified by grid searches shown in Appendix Table 1
Appendix Table 1: The hyperparameter values of the best-performing models learned from six datasets.
Figure 2 shows the side by side comparisons of the ROC curves of the four ensemble methods. It contains 4 sub-figures, one for each of the 6 PCP datasets. Based on Figure 2, all methods performed comparably for the datasets PCP-1, and PCP-2. The performance differs somewhat for datasets PCP-1, PCP-4, and PCP-5, and differs the most for dataset PCP-6. Figure 3 shows the boxplots we generated to compare side by side the prediction performance of all methods based on the mean and standard deviation of mean testing AUCs resulted from 5-fold cross-validation across all hyperparameter settings of the grid search.
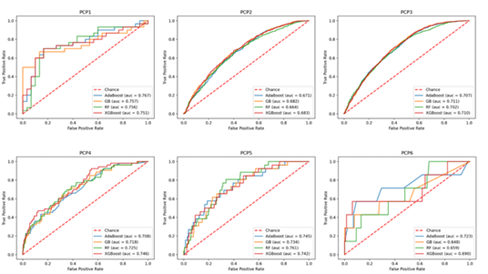
Figure 2: ROC curves of different best models selected by grid search
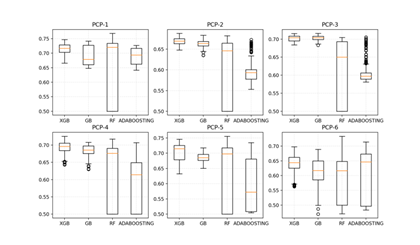
Figure 3: Mean test AUCs of all methods for each of the datasets
|
PCP-1 |
PCP-2 |
PCP-3 |
PCP-4 |
PCP-5 |
PCP-6 |
Average |
|
|
RF |
0.704 |
0.665 |
0.698 |
0.719 |
0.732 |
0.718 |
0.706 |
|
ADB |
0.767 |
0.671 |
0.707 |
0.708 |
0.745 |
0.723 |
0.72 |
|
GB |
0.693 |
0.682 |
0.711 |
0.704 |
0.691 |
0.65 |
0.689 |
|
XGB |
0.747 |
0.683 |
0.716 |
0.746 |
0.742 |
0.69 |
0.721 |
|
Average |
0.728 |
0.675 |
0.708 |
0.719 |
0.728 |
0.695 |
0.709 |
|
Maximum |
0.767 |
0.683 |
0.716 |
0.746 |
0.745 |
0.723 |
0.721 |
Table 3: The validation AUCs of the best-performing models recommended by grid search
|
RF |
ADB |
GB |
XGB |
|
|
PCP-1 (sec) |
0.315 |
0.969 |
5.308 |
322.697 |
|
PCP-2 (sec) |
2.309 |
21.539 |
169.597 |
348.412 |
|
PCP-3 (sec) |
3.714 |
37.987 |
307.798 |
1134.892 |
|
PCP-4 (sec) |
1.707 |
14.369 |
158.285 |
455.265 |
|
PCP-5 (sec) |
1.187 |
11.746 |
126.562 |
404.557 |
|
PCP-6 (sec) |
0.426 |
2.167 |
19.597 |
261.493 |
|
# of Models Trained |
864000 |
7200 |
1620 |
21870 |
|
Total Time (day) |
16.1 |
1 |
2.5 |
123.5 |
Table 4: Experiment time per model, number of models trained, and total running time
|
two-tailed |
W |
p-value |
95% confidence |
|
RF vs ADB |
12 |
0.3939 |
[-0.049, 0.025] |
|
RF vs GB |
27.5 |
0.1488 |
[-0.01301250, 0.04803801] |
|
RF vs XGB |
13 |
0.4848 |
[-0.048, 0.028] |
|
ADB vs GB |
29 |
0.09307 |
[-0.004, 0.073] |
|
ADB vs XGB |
17 |
0.9372 |
[-0.039, 0.040] |
|
GB vs XGB |
8 |
0.132 |
[-0.064, 0.008] |
Table 5: Two-sided Wilcoxon Rank-Sum Test
|
greater |
W |
p-value |
95% confidence |
|
RF vs ADB |
12 |
0.8452 |
[-0.047, inf] |
|
RF vs GB |
27.5 |
0.07441 |
[-0.006072549, inf] |
|
RF vs XGB |
13 |
0.803 |
[-0.043, inf] |
|
ADB vs RF |
24 |
0.197 |
[-0.012, inf] |
|
ADB vs GB |
29 |
0.04654 |
[0.003, inf] |
|
ADB vs XGB |
17 |
0.5909 |
[-0.038, inf] |
|
GB vs RF |
8.5 |
0.9457 |
[-0.03900343, inf] |
|
GB vs ADB |
7 |
0.9675 |
[-0.063, inf] |
|
GB vs XGB |
8 |
0.9535 |
[-0.056, inf] |
|
XGB vs RF |
23 |
0.2424 |
[-0.016, inf] |
|
XGB vs ADB |
19 |
0.4686 |
[-0.029, inf] |
|
XGB vs GB |
28 |
0.06602 |
[-0.001, inf] |
Table 6: One-sided Wilcoxon Rank-Sum Test
As shown in Table 5, we conducted two-sided pair-wise Wilcoxson rank-sum tests among the four ensemble methods. Based on this table, at a significance level of 0.05, none of the p-values is small enough for us to reject the null hypothesis, which states that the two comparison methods perform the same. However, when we raise the significance level to 0.1, we are confident in rejecting the null hypothesis for the pair of ADB and GB. When we raise the significance level to 0.15, we are confident in rejecting the null hypothesis for the pairs of XGB and GB, and RF and GB. So based on Table 5, no evidence shows that the four methods perform differently when we allow up to 5% chance of type I error, but when we allow higher error rates, we are more confident in stating that GB performs differently from the other three methods. Table 6 contains our one-sided pair-wise Wilcoxson rank-sum test results. Based on Table 6, at the significance level of 0.05, ADB performed better than GB. At the significance level of 0.1, we are confident that both XGB and RF perform better than GB. Both Table 5 and Table 6 show XGB, ADB, and RF do not perform differently when the type 1 error rate is not allowed to exceed 5%. However, based on Table 6, when we allowed the type I error rate to be as high as 25%, both XGB and ADB would perform significantly better than RF. Therefore, our statistical testing results show that XGB and ADB overall perform the same, and they both perform significantly better than RF if we allow up to 25% change for type 1 error. When we allow up to 10% error rate, we are confident that GB is the worst performer among all methods. Based on the p-values found in Table 5 and Table 6, we rank these 4 methods as follows: XGB≈ADB>RF>GB.
We also compared the ensemble methods with some of the non-ensemble methods including Naïve Base (NB), Logistic Regression (LR), Decision Trees (DT), Support Vector Machine (SVM), LASSO, and k-Nearest Neighbor (KNN). Table 7 shows the validation AUC results we obtained for the six non-ensemble methods using grid search. Appendix Table 2 shows all the 24 two-sided pair-wise Wilcoxon rank-sum test results between the 4 ensemble and the 6 non-ensemble. Based on this table, at the significance level of 0.1, we found the following pairs performed significantly differently (bold): RF vs NB, RF vs DT, ADB vs NB, ADB vs DT, GB v DT, XGB vs NB, XGB vs DT, and XGB vs KNN. When a two-sided pairwise test showed significant results, we further conducted a one-sided (greater than) pair-wise Wilcoxon rank-sum test for the corresponding pair. These results are contained in Table 8.
|
Two-sided |
W |
p-value |
95% confidence |
|
RF vs NB |
29 |
0.09307 |
[-0.026, 0.116] |
|
RF vs LR |
21.5 |
0.6304 |
[-0.03901531, 0.18101214] |
|
RF vs DT |
35 |
0.004329 |
[0.021, 0.082] |
|
RF vs SVM |
16 |
0.8182 |
[-0.052, 0.045] |
|
RF vs LASSO |
22.5 |
0.5211 |
[-0.03304188, 0.17704976] |
|
RF vs KNN |
23 |
0.4848 |
[-0.034, 0.101] |
|
ADB vs NB |
30 |
0.06494 |
[-0.013, 0.148] |
|
ADB vs LR |
26 |
0.2403 |
[-0.035, 0.187] |
|
ADB vs DT |
35 |
0.004329 |
[0.027, 0.112] |
|
ADB vs SVM |
18 |
1 |
[-0.047, 0.054] |
|
ADB vs LASSO |
26 |
0.2403 |
[-0.028, 0.183] |
|
ADB vs KNN |
27 |
0.1797 |
[-0.03, 0.12] |
|
GB vs NB |
26 |
0.2403 |
[-0.047, 0.101] |
|
GB vs LR |
19 |
0.9372 |
[-0.055, 0.106] |
|
GB vs DT |
32 |
0.02597 |
[0.007, 0.067] |
|
GB vs SVM |
10 |
0.2403 |
[-0.075, 0.030] |
|
GB vs LASSO |
19 |
0.9372 |
[-0.053, 0.162] |
|
GB vs KNN |
23 |
0.4848 |
[-0.051, 0.085] |
|
XGB vs NB |
29 |
0.09307 |
[-0.011, 0.134] |
|
XGB vs LR |
24 |
0.3939 |
[-0.027, 0.199] |
|
XGB vs DT |
35 |
0.004329 |
[0.035, 0.105] |
|
XGB vs SVM |
22 |
0.5887 |
[-0.036, 0.068] |
|
XGB vs LASSO |
25 |
0.3095 |
[-0.019, 0.195] |
|
XGB vs KNN |
29 |
0.09307 |
[-0.022, 0.119] |
Appendix Table 2: Two-sided Wilcoxon Rank-Sum Test on Ensemble Methods vs ML Methods
|
PCP-1 |
PCP-2 |
PCP-3 |
PCP-4 |
PCP-5 |
PCP-6 |
|
|
NB |
0.758 |
0.619 |
0.659 |
0.653 |
0.686 |
0.549 |
|
LR |
0.748 |
0.635 |
0.665 |
0.702 |
0.743 |
0.484 |
|
DT |
0.684 |
0.623 |
0.651 |
0.655 |
0.644 |
0.637 |
|
SVM |
0.726 |
0.674 |
0.713 |
0.725 |
0.658 |
0.77 |
|
LASSO |
0.751 |
0.636 |
0.665 |
0.697 |
0.735 |
0.488 |
|
KNN |
0.738 |
0.647 |
0.678 |
0.624 |
0.597 |
0.744 |
Table 7: Validation Score of ML Methods
To further understand a dataset influences ensemble learning, we grouped the 6 datasets in terms of both data imbalance and the size of the data. Based on data balance, we created two groups: PCP-1, PCP-2, and PCP-3 belong to the balanced group, and PCP-4, PCP-5, and PCP-6 belong to the imbalanced group. The comparison between these two groups is shown in Figure 4. Based on the size of the data, we created large-scale and small-scale groups. The large scale group contains PCP-2, PCP-3, PCP-4 and PCP-5, and the small-scaled group contains PCP-1 and PCP-6. The comparison between these two groups is shown in Figure 5.
|
Greater |
W |
p-value |
95% confidence |
|
RF vs NB |
29 |
0.04654 |
[0.006, inf] |
|
RF vs DT |
35 |
0.002165 |
[0.034, inf] |
|
RF vs KNN |
23 |
0.2424 |
[-0.025, inf] |
|
ADB vs NB |
30 |
0.03247 |
[0.012, inf] |
|
ADB vs DT |
35 |
0.002165 |
[0.039, inf] |
|
ADB vs KNN |
27 |
0.08983 |
[-0.015, inf] |
|
GB vs NB |
26 |
0.1201 |
[-0.009, inf] |
|
GB vs DT |
32 |
0.01299 |
[0.013, inf] |
|
GB vs KNN |
23 |
0.2424 |
[-0.045, inf] |
|
XGB vs NB |
29 |
0.04654 |
[0.004, inf] |
|
XGB vs DT |
35 |
0.002165 |
[0.039, inf] |
|
XGB vs KNN |
29 |
0.04643 |
[0.002, inf] |
Table 8: One-sided Wilcoxon Rank-Sum Test on Ensemble Methods vs ML Methods
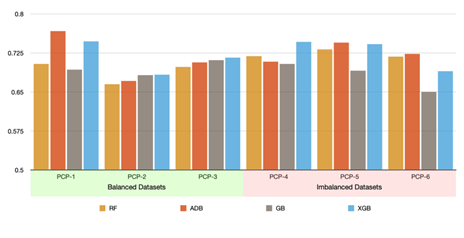
Figure 4: Performance comparison of balanced vs. imbalanced datasets
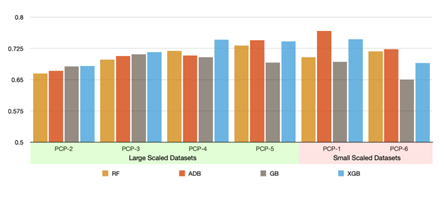
Figure 5: Performance comparison of large-scale and small-scale datasets
4. Discussion
As shown in the results section, we compared the prediction performance of the four ensemble methods. GB comes with the worst validation AUC (with PCP-6) among all methods and datasets. Our statistical tests also show that GB tends to perform worst among all methods. This is perhaps because GB is one of the earlier and therefore less mature boosting methods. As shown in Figure 4 and 5, we investigated the possible effect of the dataset itself on the performance of a method. We notice that GB tends to perform comparably with other ensemble methods for large and balanced datasets such as PCP-2 and PCP-3. For small-scale and/or imbalanced datasets such as PCP-1 and -6, GB tends to perform the worst. This may indicate that GB is less adaptive to data scarcity and imbalance. We notice that GB has a less number of hyperparameters than the later boosting methods such as ADB and XGB. It may be in the lack of hyperparameters that can be tuned to adapt to unfavorable data conditions.
Our results also show that ADB and XGB are overall very comparable in terms of their prediction performance, and each leads for three of the six datasets; that is, ADB performs the best with PCP-1, PCP-5, and PCP-6; while XGB performs the best with PCP-2, PCP-3, and PCP-4. We also found that both ADB and XGB perform better than RF in most cases. As shown by Figure 3, XGB and GB can provide much stable results in all datasets regardless of what hyperparameter values are given, while RF’s interquartile ranges are the largest across all datasets, which can range from 0.5 up to 0.75. ADB has a mixed situation: it has a stabler performance for dataset PCP-1, PCP-2, and PCP-3 than it does for dataset PCP-4 through PCP-6.
We also compared the ensemble methods with some of the non-ensemble methods including NB, LR, DT, SVM, LASSO, and KNN. Based on results, XGB performs significantly better than KNN, XGB, ADB, and RF perform significantly better than both NB and DT, and all ensemble methods perform better than DT. So, XGB performs better than most of the non-ensemble methods that we included in the study, ADB and RF performs better than half of the non-ensemble methods included. Even GB, the ensemble method that did the worst in this study, performed significantly better than DT. However, on the other hand, we notice that the non-ensemble methods SVM and LASSO, when using grid search, perform comparably with all the ensemble methods. The non-ensemble method KNN performs comparably with three of the four ensemble methods.
We also looked into how these ensemble methods perform differently in terms of a specific dataset by paying attention to data scarcity and imbalance issues. We notice from Table 3 that ADB, even though ranks No. 2 on average, can achieve a validation AUC as high as 0.767 (with PCP-1), which is the highest score we ever obtained using these PCP datasets. In terms of PCP-6, a small and imbalanced dataset, again ADB and XGB outperformed the other two, and ADB reached a validation AUC of 0.723, which is the highest we observed for PCP-6.
Based on Figure 4 and 5, XGB outperforms ADB for all datasets except for datasets PCP-1, and PCP-6. Note that PCP-1 and PCP-6 are the two small-scale datasets; this may indicate that ADB tends to handle small-scale datasets better than XGB. RF performs worse than XGB for all the datasets except for PCP-6, which is both a small-scale and imbalanced dataset. This may indicate that RF tends to handle this type of dataset better than XGB. Based on Figure 4, we also notice that RF tends to perform better with the imbalanced datasets than it does with the balanced datasets.
Grid search helps greatly to identify the best hyperparameter setting for each method by training a large number of models. Based on Table 5, RF is the method for which the largest number of models are trained in grid search. This is because RF has more hyperparameters than other methods. However, as shown in Table 5, it takes the least amount of time to train a model with RF among all methods. RF ends up being No. 2 in terms of the total amount of time it takes to run the grid search. ADB takes the least amount of time for grid search, because it is relative fast to train a ADB model and the total number of ADB models trained in grid search is way less than RF. XGB is the bottleneck in terms of grid search running time among all methods. This is because its unit model training times are the longest and the number of models trained in grid search ranks at No. 2 among all methods.
5. Conclusion
Based on this study, ensemble is a promising way of improving Ubiquitination-site prediction using PCP data. We find that all four ensemble methods significantly outperform one or more non-ensemble methods included in this study. XGB outperforms 3 out of the 6 non-ensemble methods that we included; ADB and RF both outperform 2 of the 6 non-ensemble methods included. GB performs better than one non-ensemble method. Comparing the four ensemble methods internally, GB performs the worst; XGB and ADB are very comparable in terms of prediction. But ADB beats XGB by far in terms of both the unit model training time and total running time (ADB’s 1 day vs XGB’s 123 days). Both XGB and ADB tend to do better than RF in terms of prediction, but RF has the shortest unit model training time out of the three. In addition, we notice that ADB tends to outperform XGB when dealing with small-scale datasets, and RF can outperform either ADB or XGB when data are less balanced. Interestingly, we find that SVM, LR, and LASSO, three of the non-ensemble methods included, perform comparably with all the ensemble methods.
Author’s Contributions
Conceptualization, XJ; methodology, XM and XJ; software, XJ; validation, XM and XJ; formal analysis, XM and XJ; investigation, XJ; resources, XJ; data curation, N/A; writing-original draft preparation, XM and XJ; writing-review and editing, XM and XJ; visualization, N/A; supervision, XJ; project administration, XJ; funding acquisition, XJ; All authors have read and agreed to the published version of the manuscript.
Funding
Research reported in this paper was supported by the U.S. Department of Defense through the Breast Cancer Research Program under Award No. W81XWH1910495 (to XJ). Other than supplying funds, the funding agencies played no role in the research.
Data Availability
The datasets used and/or analyzed during the current study are existing datasets previously published at
https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-016-0959-z
References
- Bosch A. van den Hengst B, et al. Hypothesis Space. In Encyclopedia of Machine Learning; Springer US: Boston, MA 11(2011): 511-513.
- Ali KM, Pazzani MJ. Error Reduction through Learning Multiple Descriptions. Mach Learn 24 (1996).
- Husmeier D, Althoefer K. Modelling Conditional Probabilities with Network Committees: How Overfitting Can Be Useful. Neural Network World 8 (1998).
- Kuncheva LI, Whitaker CJ. Measures of Diversity in Classifier Ensembles and Their Relationship with the Ensemble Accuracy. Mach Learn 51 (2008).
- Brown G, Wyatt J, Harris R, et al. Diversity Creation Methods: A Survey and Categorisation. Information Fusion 6 (2005).
- Garcia Adeva JJ, Cervino Beresi U, Calvo RA. Accuracy and Diversity in Ensembles of Text Categorisers. CLEI Electronic Journal 8 (2005)
- Ho TK. Random Decision Forests. In Proceedings of the Proceedings of the International Conference on Document Analysis and Recognition, ICDAR 1 (1995)
- Gashler M, Giraud-Carrier C, Martinez T. Decision Tree Ensemble: Small Heterogeneous Is Better Than Large Homogeneous 7(2009).
- Zhou ZH. Ensemble Methods: Foundations and Algorithms 10(2012).
- Fernández-Delgado M, Cernadas E, Barro S, et al. Do We Need Hundreds of Classifiers to Solve Real World Classification Problems? Journal of Machine Learning Research 15 (2014).
- Dietterich TG. Ensemble Methods in Machine Learning. In Proceedings of the Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 8(2000).
- Polikar R. Ensemble Based Systems in Decision Making. IEEE Circuits and Systems Magazine 6 (2006).
- Zhang J. Developing Robust Non-Linear Models through Bootstrap Aggregated Neural Networks. Neurocomputing 25 (1999).
- Svetnik V, Liaw A, Tong C, et al. Random Forest: A Classification and Regression Tool for Compound Classification and QSAR Modeling. J Chem Inf Comput Sci 43 (2003).
- Mordelet F, Vert JP. A Bagging SVM to Learn from Positive and Unlabeled Examples. Pattern Recognit Lett 37(2014).
- Aslam JA, Popa RA, Rivest, RL. On Estimating the Size and Confidence of a Statistical Audit. In Proceedings of the EVT 2007 - 2007 USENIX/ACCURATE Electronic Voting Technology Workshop 13 (2007).
- Bauer E, Kohavi R. Empirical Comparison of Voting Classification Algorithms: Bagging, Boosting, and Variants. Mach Learn 36 (1999)
- Freund Y, Schapire RE. Experiments with a New Boosting Algorithm. Proceedings of the 13th International Conference on Machine Learning 7(1996).
- Schapire RE. The Strength of Weak Learnability. Mach Learn 5 (1990).
- Kearns M, Valiant LG. Cryptographic Limitations on Learning Boolean Formulae and Finite Automata 23 (1989).
- Dietterich TG. Experimental Comparison of Three Methods for Constructing Ensembles of Decision Trees: Bagging, Boosting, and Randomization. Mach Learn 40 (2000).
- Herrmann J, Lerman LO, Lerman A. Ubiquitin and Ubiquitin-like Proteins in Protein Regulation. Circ Res 100 (2007).
- Welchman RL, Gordon C, Mayer RJ. Ubiquitin and Ubiquitin-like Proteins as Multifunctional Signals. Nat Rev Mol Cell Biol 6 (2005).
- Tung CW, Ho SY. Computational Identification of Ubiquitylation Sites from Protein Sequences. BMC Bioinformatics 9 (2008)
- Walsh I, di Domenico T, Tosatto SCE. RUBI: Rapid Proteomic-Scale Prediction of Lysine Ubiquitination and Factors Influencing Predictor Performance. Amino Acids 46 (2014).
- Peng J, Schwartz D, Elias JE, et al. A Proteomics Approach to Understanding Protein Ubiquitination. Nat Biotechnol 21 (2003).
- Kirkpatrick, D.S., Denison, C., Gygi, S.P. Weighing in on Ubiquitin: The Expanding Role of Mass-Spectrometry-Based Proteomics. Nat Cell Biol. 7 (2005).
- Wagner SA, Beli P, Weinert BT, et al. A Proteome-Wide, Quantitative Survey of in Vivo Ubiquitylation Sites Reveals Widespread Regulatory Roles. Molecular and Cellular Proteomics 5(2011).
- Xu G, Paige JS, Jaffrey SR. Global Analysis of Lysine Ubiquitination by Ubiquitin Remnant Immunoaffinity Profiling. Nat Biotechnol 28 (2010).
- Kim, W, Bennett EJ, Huttlin EL, et al. Systematic and Quantitative Assessment of the Ubiquitin-Modified Proteome. Mol Cell 44 (2011).
- Radivojac P, Vacic V, Haynes C, et al. Identification, Analysis, and Prediction of Protein Ubiquitination Sites. Proteins: Structure, Function and Bioinformatics 78 (2010).
- Cai Y, Huang T, Hu L, et al. Prediction of Lysine Ubiquitination with MRMR Feature Selection and Analysis. Amino Acids 42 (2012).
- Chen Z, Zhou Y, Zhang Z, et al. Towards More Accurate Prediction of Ubiquitination Sites: A Comprehensive Review of Current Methods, Tools and Features. Brief Bioinform 16 (2014).
- Cai B, Jiang X. Computational Methods for Ubiquitination Site Prediction Using Physicochemical Properties of Protein Sequences. BMC Bioinformatics 17 (2016).
- Breiman L. Random Forests. Mach Learn 45 (2001).
- Cutler DR, Edwards TC, Beard KH, et al. Random Forests for Classification in Ecology. Ecology 88 (2007).
- Chen Z, Han F, Wu L, et al. Random Forest Based Intelligent Fault Diagnosis for PV Arrays Using Array Voltage and String Currents. Energy Convers Manag 178 (2018),
- Freund Y, Schapire RE. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J Comput Syst Sci 55 (1997)
- Friedman JH. Greedy Function Approximation: A Gradient Boosting Machine. Ann Stat 29 (2001),
- Chen T, He T. Xgboost: Extreme Gradient Boosting. R Lecture 9 (2014).
- Friedman JH. Stochastic Gradient Boosting. Comput Stat Data Anal 38 (2002).
- Dietterich TG. Machine-Learning Research: Four Current Directions. AI Mag 18 (1997).
- Chen T, Guestrin C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 13 (2016).
- Schapire RE. Explaining Adaboost. In Empirical Inference: Festschrift in Honor of Vladimir N. Vapnik 7 (2013).
- Galar M, Fernandez A, Barrenechea E, et al. A Review on Ensembles for the Class Imbalance Problem: Bagging-, Boosting-, and Hybrid-Based Approaches. IEEE Transactions on Systems, Man and Cybernetics Part C: Applications and Reviews 42 (2012).
- Opitz D, Maclin R. Popular Ensemble Methods: An Empirical Study. Journal of Artificial Intelligence Research 11 (1999)
- Viola P, Jones MJ. Robust Real-Time Face Detection. Int J Comput Vis 57 (2004).
- Viola, P., Jones, M. Rapid Object Detection Using a Boosted Cascade of Simple Features. In Proceedings of the Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition 1 (2001).
- Breiman L. Arcing the Edge. Statistics (Ber) 4(1997).
- Mason L, Baxter J, Bartlett P, et al. Boosting Algorithms as Gradient Descent in Function Space. Nips 15 (1999).
- Mason L, Baxter J, Bartlett P, et al. Boosting Algorithms as Gradient Descent. In Proceedings of the Advances in Neural Information Processing Systems 10 (2000).
- Xia Y, Liu C, Li YY, et al. A Boosted Decision Tree Approach Using Bayesian Hyper-Parameter Optimization for Credit Scoring. Expert Syst Appl 78 (2017): 225-241.
- Ribeiro M H D M, dos Santos Coelho L. Ensemble Approach Based on Bagging, Boosting and Stacking for Short-Term Prediction in Agribusiness Time Series. Applied Soft Computing Journal 86 (2020),
- Yang L, Shami A. On Hyperparameter Optimization of Machine Learning Algorithms: Theory and Practice. Neurocomputing 415 (2020)
- Bergstra J, Bengio Y. Random Search for Hyper-Parameter Optimization. Journal of Machine Learning Research 13 (2012).
- Pedregosa F, Varoquaux G, Gramfort A, et al. Scikit-Learn: Machine Learning in Python. Journal of Machine Learning Research 12 (2011).
- Belete, D.M, Huchaiah, M.D. Grid Search in Hyperparameter Optimization of Machine Learning Models for Prediction of HIV/AIDS Test Results. International Journal of Computers and Applications 44 (2021): 875-886.
- Ghawi, R, Pfeffer, J. Efficient Hyperparameter Tuning with Grid Search for Text Categorization Using KNN Approach with BM25 Similarity. Open Computer Science 9 (2019).
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit Lett 27 (2006).
