Detection of Breast Cancer in Infrared Thermographies Using Stochastic Techniques in a FPGA Platform
Article Information
J. de la Cruz-Alejo*, Irving Cardiel Alcocer Guillermo, M. B. Arce Vázquez, Ernesto Enciso Contreras
Mechatronic Department, Tecnológico de Estudios Superiores de Ecatepec, Ecatepec, Estado de México
*Corresponding Author: J. de la Cruz-Alejo, Mechatronic Department, Tecnológico de Estudios Superiores de Ecatepec, Ecatepec, Estado de México
Received: 21 February 2020; Accepted: 20 April 2020; Published: 17 Augst 2020
Citation: J. de la Cruz-Alejo, Irving Cardiel Alcocer Guillermo, M. B. Arce Vázquez, Ernesto Enciso Contreras. Detection of Breast Cancer in Infrared Thermographies Using Stochastic Techniques in a FPGA Platform. Journal of Bioinformatics and Systems Biology 3 (2020): 045-057.
Share at FacebookAbstract
Thermo graphical infrared images to predict the existence of a thermal anomaly according to symmetry in breasts by using stochastic methods and fuzzy logic control is proposed. Statistical results are established through entropy, kurtosis and media to evaluate symmetry grade between the right and left breast. To predict the grade of breast cancer associated to the tissue and take a decision a fuzzy controller is designed in base to symmetric assessments distribution. The proposed method is implemented on a FPGA platform optimizing hardware requirements and improves response time. Results show that the error of the prediction method can be an alternative to detect cancer if the image source are far away from the critical errors, interference to the source or infrared image processed.
Keywords
Infrared images; FPGA; Stochastic methods; Fuzzy controller breast cancer
Infrared images articles, FPGA articles, Stochastic methods articles, Fuzzy controller breast cancer articles
Infrared images articles Infrared images Research articles Infrared images review articles Infrared images PubMed articles Infrared images PubMed Central articles Infrared images 2023 articles Infrared images 2024 articles Infrared images Scopus articles Infrared images impact factor journals Infrared images Scopus journals Infrared images PubMed journals Infrared images medical journals Infrared images free journals Infrared images best journals Infrared images top journals Infrared images free medical journals Infrared images famous journals Infrared images Google Scholar indexed journals FPGA articles FPGA Research articles FPGA review articles FPGA PubMed articles FPGA PubMed Central articles FPGA 2023 articles FPGA 2024 articles FPGA Scopus articles FPGA impact factor journals FPGA Scopus journals FPGA PubMed journals FPGA medical journals FPGA free journals FPGA best journals FPGA top journals FPGA free medical journals FPGA famous journals FPGA Google Scholar indexed journals Stochastic methods articles Stochastic methods Research articles Stochastic methods review articles Stochastic methods PubMed articles Stochastic methods PubMed Central articles Stochastic methods 2023 articles Stochastic methods 2024 articles Stochastic methods Scopus articles Stochastic methods impact factor journals Stochastic methods Scopus journals Stochastic methods PubMed journals Stochastic methods medical journals Stochastic methods free journals Stochastic methods best journals Stochastic methods top journals Stochastic methods free medical journals Stochastic methods famous journals Stochastic methods Google Scholar indexed journals Fuzzy controller breast cancer articles Fuzzy controller breast cancer Research articles Fuzzy controller breast cancer review articles Fuzzy controller breast cancer PubMed articles Fuzzy controller breast cancer PubMed Central articles Fuzzy controller breast cancer 2023 articles Fuzzy controller breast cancer 2024 articles Fuzzy controller breast cancer Scopus articles Fuzzy controller breast cancer impact factor journals Fuzzy controller breast cancer Scopus journals Fuzzy controller breast cancer PubMed journals Fuzzy controller breast cancer medical journals Fuzzy controller breast cancer free journals Fuzzy controller breast cancer best journals Fuzzy controller breast cancer top journals Fuzzy controller breast cancer free medical journals Fuzzy controller breast cancer famous journals Fuzzy controller breast cancer Google Scholar indexed journals Stochastic Techniques articles Stochastic Techniques Research articles Stochastic Techniques review articles Stochastic Techniques PubMed articles Stochastic Techniques PubMed Central articles Stochastic Techniques 2023 articles Stochastic Techniques 2024 articles Stochastic Techniques Scopus articles Stochastic Techniques impact factor journals Stochastic Techniques Scopus journals Stochastic Techniques PubMed journals Stochastic Techniques medical journals Stochastic Techniques free journals Stochastic Techniques best journals Stochastic Techniques top journals Stochastic Techniques free medical journals Stochastic Techniques famous journals Stochastic Techniques Google Scholar indexed journals fuzzy articles fuzzy Research articles fuzzy review articles fuzzy PubMed articles fuzzy PubMed Central articles fuzzy 2023 articles fuzzy 2024 articles fuzzy Scopus articles fuzzy impact factor journals fuzzy Scopus journals fuzzy PubMed journals fuzzy medical journals fuzzy free journals fuzzy best journals fuzzy top journals fuzzy free medical journals fuzzy famous journals fuzzy Google Scholar indexed journals Linguistic variables articles Linguistic variables Research articles Linguistic variables review articles Linguistic variables PubMed articles Linguistic variables PubMed Central articles Linguistic variables 2023 articles Linguistic variables 2024 articles Linguistic variables Scopus articles Linguistic variables impact factor journals Linguistic variables Scopus journals Linguistic variables PubMed journals Linguistic variables medical journals Linguistic variables free journals Linguistic variables best journals Linguistic variables top journals Linguistic variables free medical journals Linguistic variables famous journals Linguistic variables Google Scholar indexed journals transcriptomics articles transcriptomics Research articles transcriptomics review articles transcriptomics PubMed articles transcriptomics PubMed Central articles transcriptomics 2023 articles transcriptomics 2024 articles transcriptomics Scopus articles transcriptomics impact factor journals transcriptomics Scopus journals transcriptomics PubMed journals transcriptomics medical journals transcriptomics free journals transcriptomics best journals transcriptomics top journals transcriptomics free medical journals transcriptomics famous journals transcriptomics Google Scholar indexed journals
Article Details
1. Introduction
Currently there are several methods to detect cancer, which can detect its appearance and more likely to treat it successfully. Detection methods most commonly used today require complex machines that do not give a result to the naked eye, but these need to be analyzed by a specialist. These methods are invasive and need machines too expensive. Also, a thermo graphical record of an individual's body can be created and processed for further analysis to determine the existence of a thermal anomaly. Also, image segmentation involves the use of various techniques to extract and separate relevant information from an image. [1-7]. Stochastic techniques can be used for detection thermal anomalies, more precisely thermal asymmetry in the chest area to detect cancer. In the other hand, novel fuzzy control methods have been developed and implemented as a programming platform to control different processes in different areas. Due to their heuristic nature associated with simplicity and effectiveness for both linear and non-linear systems, fuzzy logic controllers (FLC) has showed their outstanding features in implementations for solar tracking systems, mechatronics systems, etc. [8-13].
The main aim of this paper is to use stochastic techniques and fuzzy logic controller to detect the thermal asymmetry in the region in a simple and precise way in comparison to the already existing techniques of breast cancer detection.
The structure of rest of the paper is as follow. Section 2, describe the stochastic processes of the termographical images in order to elaborate a stochastic approach for detecting the breast cancer. In Section 3, based on the stochastic approach, the grade of breast cancer is determined according to a fuzzy control as alternative to manage the stochastic information. Section 4, shows the characterization of this propose by simulation and experimental results. The paper concludes with Section 4, where conclusions are drawn.
2. Stochastic techniques for detection thermal asymmetries
Figure 1, represents in a modular way the processes to be performed for the breast cancer detection based on thermographic images. The first block refers to a thermal image obtained by a device outside the system which is a thermographic camera. Once the thermographic image is obtained, it is processed by a conversion to grayscale taking the luminance of the pixels, a segmentation to separate the background of the image and the information that correspond to the chest on which the study will be performed. Then, since the body symmetry must be identified, the main image is divided in two sub-images. These sub-images contain only the tissue corresponding to the left and right chest. Next, stochastic techniques are applied to each breast to determine the asymmetry grade between these two images without considering the size of the samples. Finally, Linguistic variables are proposed to design the fuzzy control to determine the grade of breast cancer associated to the tissue.
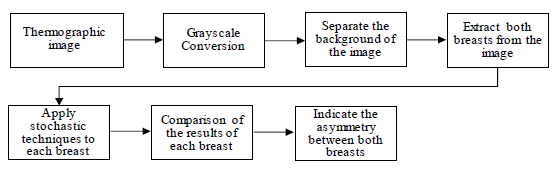
Figure 1: Schematic diagram proposed to detect breast cancer using stochastic techniques.
2.1 Grayscale conversion
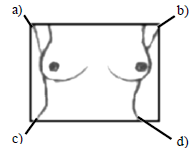
To convert the grayscale image, first it is separated into three spectra information RGB. Once the image is separated, it is converted to gray scale and processed to normalize the image values. This consists in establishing a minimum reference pixel value which will be used to represent different temperatures in the human tissue. Eliminating background noise in the image, it is segmented in order to isolate both breast tissues and find some key points within the image which are able to provide where begins and ends in the thermal image. Figure 2, shows the key points locations represented by: Top Right Point (TRP), Left Upper Point (LUP), Right Lower Point (RLP), Left Lower Point (LLP). The first point (TRP), is find through locating the first pixel not belonging to the bottom of the image, starting with the top left of the image, using:
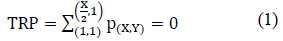
Where X represents the total width of the image and determines the beginning of the body in the image and Y, represents the total height of the image measured from top to bottom.
In similar way is found the second point (LUP), only that the counting starts from the pixel (1, X), which would be the top row and the final column of the image. Third point (RLP), start with the first pixel at the left bottom (Y, 1). It starts counting the number of zeros that are in this row from left to right until it reaches X / 2, which is the half of the image, using:
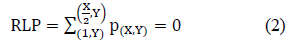
Finally the fourth point (LLP), represent the first pixel corresponding to the left side of the body in the thermal image. It consists in counting the pixels belonging to the bottom of the image or zero value, starting from the lower left (X, Y), using:
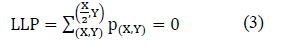
Once the four main points of the image are found, lines are drawn to joins the points TRP with LLP and LUP with RLP, as is shown in Figure 3. The intersection of both points will be called the geometric center (GC). To obtain this point, is necessary to determine the angles shown in Figure 4.

Figure 3 and Figure 4:
The angle of the line joining the points LUP and RLP is called α. To determine the value of this angle, the distance between these points on the horizontal axis X is obtained, using:
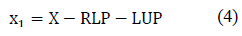
Then, angle α is calculated by:
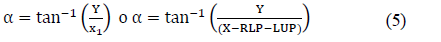
Same manner, angle called β, corresponding to the line joining the points TRP and LLP is obtained by:
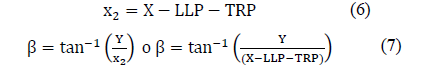
Third angle φ, is obtained by:
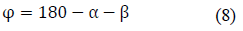
Considering the angles β and φ in addition to the distance from RLP to LLP, which forms the total base of the triangle, the distance from RLP to GC called DC, is found by:
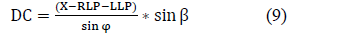
Distance from LLP to GC called LC, is found through the α and φ angles and the distance from RLP to LLP, by:

Once the distance DC and LC have been obtained, the height of the GC point called GCY is obtained by:
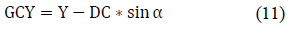
Horizontal distance of the GC, called GCX is determined by:
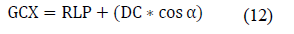
Once these points are located, the image of the breast is separate in two, right and left.
2.2. Stochastic process
Stochastic techniques are applied to the regions of interest to detect thermal asymmetry in base to the pixel values between right and left breasts. Arithmetic mean, is the first function to know thermal asymmetries which, is known as the mean sample [14, 15, 16], given by:

This value corresponds to the middle of all pixels values in a range from 0 to 255, which correspond to the maximum admissible thermal value. The mean value must be the same for both breasts. In case of an asymmetry or anomaly, mean value differs. Another function to consider, is the deviation of the pixels from the mean value called variance, given by:
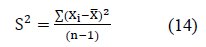
Where S2 is the variance, Σ(Xi - X -)2 is the sum of the variances for each pixel, n number of total pixels.
If the variance moves to the left (being smaller) indicates that the asymmetry is below of the average temperature, in the other case, (being greater) would indicate that the temperature is above the average. This is relevant to determine a possible cancerous tissue in anyone breast. Another function is the kurtosis which allow to know how the pixels values are concentrated in the standard central distribution area. Kurtosis coefficient is obtained by:
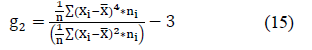
Where g2 is the kurtosis coefficient, Xi is the value of each pixel, X - is the mean and ni is the frequency at which the pixel appears.
Finally, entropy is one of the most used function for detection thermal asymmetries. When temperature distribution in both breasts is similar, the entropy value tends to be the same, and is given by:
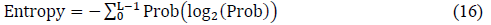
Where Prob, corresponds to the probability that a certain pixel value will appear in the image, which is represented as

2.3 Fuzzy Control
The fuzzy control structure, is designed to reduce the computational complexity, since the operations performed in each stage like multiplications, sum, divider, power, etc, are not made using hardware but look-up tables. The look-up tables play a crucial role in all stages of a Mamdani fuzzy control, and thereby, the operations tend to be very few. It is deriving from the principle of memory that the look-up tables serve to storing the membership values represented in this study by 8 bits which generate 256-levels in a binary data. Figure. 5, shows the block diagram of the Fuzzy control proposed. It consists of two inputs and one output. To convert the rigid input values to fuzzy values, data from the ADC converter act as a memory addressing while membership values are stored in look-up tables. For each rigid input value corresponding one membership value. These membership values are the input to the inference stage where they are processed through the Mamdani max-min implication, having as a result, the conclusion of the fuzzy rules. In the aggregation stage, the conclusion of each rule is combined and summed to obtain a final conclusion. Then, defuzzification stage converts the membership values to a rigid value. Finally, it is converted to a voltage using a DAC. All stages are implemented in a FPGA platform using description language VHDL code. The Output of the Fuzzy control will be the Cancer diagnosis.
2.4 Fuzzification
Input variables are defined based on the difference in the Media (DM) and Kurtosis (DK) values between the left and right breast. Each variable is represented by five fuzzy sets which conform to the linguistic variables. The fuzzy sets for the DM variable are labeled as VL (Very light), S (Small), R (Regular), L (large) and VH (Very large). The fuzzy sets for the DK variable are the same labels. The output fuzzy variable is called a cancer diagnosis (CD), and also, is represented by five fuzzy sets labeled as H (healthy), C (caution), M (minimal), D (drastic) and VD (very drastic). Each variable has a universe of discourse in the digital domain in the range from 0 to 1023, which is proposed using 10 bits of resolution. Figure. 6, shows the fuzzy sets proposed in the universe of discourse for the inputs and output variables. For the membership values, 8 bits of resolution are used, which divides the membership values in a range from 0 to 255 values, which is adequate because the range is from 0 to 1. So, each fuzzy set contain 256 levels. The base of each fuzzy set is found for those levels whose membership value is zero. This values are especially useful because they allow to know if the value of the rigid input signal belongs to a given fuzzy set.
2.5 Inference
For the inference and aggregation stages, Mamdani method is used through the max-min operations. For this, an inference matrix is generated to place the output inference values using rules If…Then by making a correlation between the membership values obtained in the fuzzification stage, using:
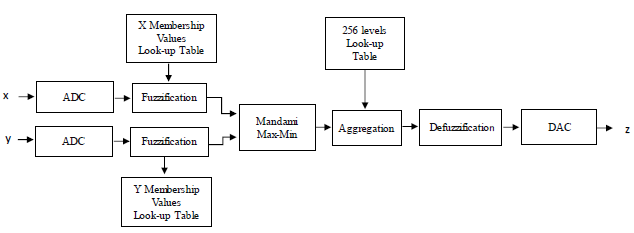
Figure 5: Block diagram of the FLC proposed.
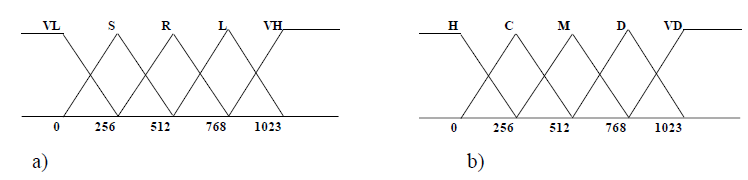
Figure 6: Membership functions for a) inputs and b) output variables.
This way, the matrix will have 25 possible output values obtained from the evaluation of the rules shown in Table I. It involves a comparison between two membership values reached in each rule and selecting the minimum membership value.
The aggregation stage is carried out by the method of maximum membership value obtained in the inference stage whose value is different to 0, given by:
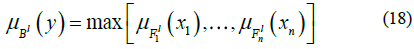
It is the union of the activated rules for each column in the matrix. In this case, five columns. It takes into account those rules that have a nonzero value. For this case, all values contained in a column are compared and selecting the maximum value and so on. These membership values fall in the universe of discourse of the output fuzzy sets call Diagnosis cancer, which are used for the defuzzification stage. This stage converts a fuzzy value to a real value.
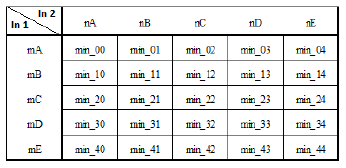
Table 1: Inference matrix.
3.3 Defuzzification
In order to save processing time and hardware on the FPGA, defuzzification with 256-levels are used to obtain the rigid output value from the aggregation vector, given by:
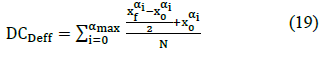
Where DCDeff is the diagnosis cancer, N, is the number of fuzzy set activated in the aggregated vector, is the final point of the level where membership value reached in the aggregated vector, is the initial point of the same level. The schematic design in VHDL for the FLC implemented is shown in Figure 7, which consist of fuzzification, inference (min), aggregation (max) and defuzzification stages.
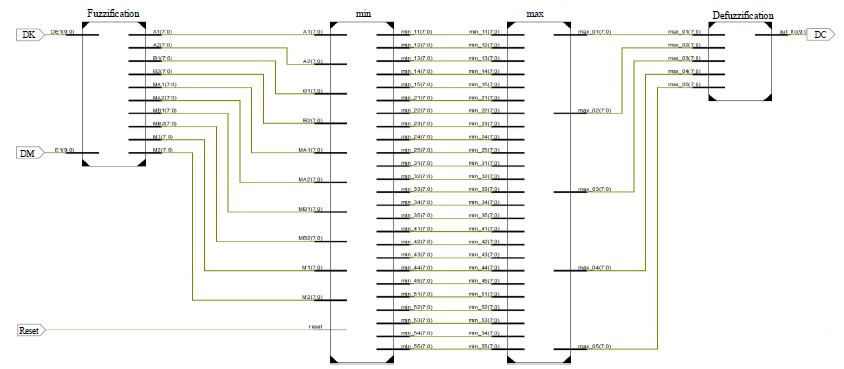
Figure 7: Schematic design for the FLC implemented.
4.Experimental Results
Measurement results were carried out taking into account a database belonging to the Visual Lab DMR (Database for Mastology Research), which is an online platform that stores mastological images for the breast cancer by your research group. Registration results of this group were compared with this proposal. To determine if the thermographs correspond to a group of healthy or cancer, a series of minimum and maximum values for the difference of Mean, Kurtosis and Entropy were taken. Also, and according to the method used by Visual Lab, the following was taking into account:
- To determine a normal thermal asymmetry, difference between average Media values belonging to the right and left breasts can have a maximum value of 3.
- Pixels distribution around the average value for each breast must be similar for both breasts. The difference between these values must not be greater than 0.63 to be considered as a normal asymmetry.
- Difference between the entropy values can be until 0.284, to determine a normal thermal asymmetry.
This manner, for diagnosing cancer, tests were performed on 44 of 72 thermographies. Tests were carried out connecting two probes to the FLC inputs through ADC cables in a digital domain according to results presented in Table II, which corresponding to the difference between Media and Kurtosis, (only 20 tests values are presented). The internal clock signal to synchronize the FLC process implemented from advanced VHDL synthesis was establish at 500 KHz. The implementation can be used for five or more linguistic variables, but can be easily expanded repeating sections of code, also can be used for any type of fuzzy set. This manner, the FLC determine thermal asymmetry between both breasts, diagnosing the grade of cancer. The experimental results were compared in a theoretical way with the method obtained by the Matlab Fuzzy Logic ToolBox. For example, considering the values of test 2, whose values are DE= 2.3199 and DK= 1.8546 introduced as inputs x and y. The digital output from the FPGA board was CAUTION whose digital value is 319, corresponding to the caution set, whereas in MatLab Fuzzy Logic ToolBox, the digital value was 333. As can be seen, the FLC implemented on the FPGA provides very approximate values to those obtained by the Matlab Fuzzy Logic ToolBox. Then, each simulation and experimental result was evaluated with respect to the Visual Lab researchers result, which was classified as healthy or cancer presented in Table III in the column named Status and in FLC/FPGA column our results. Result differs from the expert group, perhaps because the values, not represent a specific temperature since the colors are not linked to the temperatures, since these are relative to the maximum and minimum temperature of the object being photographed. As can be seen, results obtained here (with a relatively large slot of tests), fall into the healthy case where the values for the input signals representing the difference of Media and Kurtosis. This manner, 23 tests of 44, are similar to the Visual Lab group whose diagnosis were healthy, 2 were cancerous, whereas 8 were Caution, 9 were Medium and 2 were Drastic which differ from the Visual Lab group whose diagnosis were healthy. One therefore would expect little change in the diagnosis under different pixels’ distribution of the image due to its luminance parameter. Also, there would likewise be little variation in the image when some interferences are considered. Even though the results obtained cannot be ignored since difference is not greater than 15%, which tells us that the system proposed has around 85% accuracy. Finally, the mean square error (MSE) is obtained applying (20), to the data values of Table II. The MSE is 1.75%, which is very acceptable considering that this method uses iterations and 8 bits for sample.

Table 2: Theoretical stochastic values.
Table 3: Comparison between medical (VisualLab) results and those obtained in Matlab and FLC/FPGA.
|
Test |
VisualLab |
Matlab |
FLC/FPGA |
Fuzzy Set |
|
2 |
Healthy |
333 |
319 |
Caution |
|
4 |
Healthy |
128 |
127 |
Healthy |
|
6 |
Healthy |
538 |
511 |
Medium |
|
15 |
Healthy |
179 |
203 |
Healthy |
|
16 |
Healthy |
538 |
511 |
Medium |
|
20 |
Healthy |
128 |
127 |
Healthy |
|
24 |
Healthy |
128 |
127 |
Healthy |
|
26 |
Healthy |
538 |
511 |
Medium |
|
31 |
Healthy |
333 |
319 |
Healthy |
|
32 |
Healthy |
333 |
319 |
Healthy |
|
36 |
Healthy |
333 |
319 |
Healthy |
|
48 |
Healthy |
128 |
127 |
Healthy |
|
52 |
Healthy |
128 |
127 |
Caution |
|
57 |
Healthy |
128 |
127 |
Healthy |
|
62 |
Healthy |
128 |
127 |
Healthy |
|
65 |
Healthy |
742 |
703 |
Drastic |
|
66 |
Healthy |
128 |
127 |
Healthy |
|
70 |
Healthy |
538 |
511 |
Medium |
|
91 |
Healthy |
128 |
127 |
Healthy |
|
93 |
Healthy |
371 |
395 |
Caution |
|
97 |
Healthy |
333 |
319 |
Caution |
|
99 |
Healthy |
128 |
127 |
Healthy |
|
104 |
Healthy |
333 |
319 |
Caution |
|
105 |
Healthy |
128 |
127 |
Healthy |
|
106 |
Healthy |
329 |
311 |
Caution |
|
110 |
Healthy |
742 |
703 |
Drastic |
|
132 |
Healthy |
437 |
415 |
Medium |
|
135 |
Healthy |
538 |
511 |
Medium |
|
137 |
Healthy |
128 |
127 |
Healthy |
|
145 |
Healthy |
128 |
127 |
Healthy |
|
147 |
Healthy |
128 |
127 |
Healthy |
|
151 |
Healthy |
436 |
415 |
Medium |
|
152 |
Healthy |
333 |
319 |
Caution |
|
155 |
Healthy |
128 |
127 |
Healthy |
|
161 |
Healthy |
128 |
127 |
Healthy |
|
163 |
Healthy |
128 |
127 |
Healthy |
|
168 |
Healthy |
128 |
127 |
Healthy |
|
169 |
Healthy |
210 |
223 |
Healthy |
|
174 |
Healthy |
333 |
319 |
Caution |
|
180 |
Cancer |
775 |
799 |
Drastic |
|
181 |
Cancer |
333 |
319 |
Caution |
|
188 |
Healthy |
128 |
127 |
Healthy |
|
189 |
Healthy |
538 |
511 |
Medium |
|
190 |
Healthy |
538 |
511 |
Medium |
Conclusions
This paper compares and experimentally confirm breast cancer detection through the modeling, simulation, and measurement using stochastic techniques in a FPGA platform. Stochastic equations were developed for analysis of infrared images, and a fuzzy logic control was designed and implemented to illustrate the relationship to the stochastic results for detection cancer. The fuzzy controller provides very approximate values to detect at multiple grades or in a universe of discourse, different grades of cancer. Results are provided in which simulations and measurement show stable performance in the processes and in the must cases are according to the Visual Lab group diagnosing. The technique has a high percentage of accuracy in terms of cancer detection.
References
- Benmazou, Sarah, and Hayet Farida Merouani. Wavelet based feature extraction method for breast cancer diagnosis. Advanced Technologies for Signal and Image Processing (ATSIP), 2018 4th International Conference on. IEEE, 2018.
- Guan, Shuyue, and Murray Loew. Breast Cancer Detection Using Transfer Learning in Convolutional Neural Networks. 2017 IEEE Applied Imagery Pattern Recognition Workshop (AIPR). IEEE, 2017.
- Breast Cancer Detection Via Wavelet Energy and Support Vector Machine. 2018 27th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN). IEEE, 2018.
- Li, Y., et al. A survey of computer-aided detection of breast cancer with mammography. J Health Med Inform7 (2016).
- Hoseini, Farnaz, et al. A parallel implementation of modified fuzzy logic for breast cancer detection. Journal of Advances in computer Research (2016): 139-148.
- Manogaran, Gunasekaran, et al. Machine learning based big data processing framework for cancer diagnosis using hidden Markov model and GM clustering. Wireless personal communications102 (2018): 2099-2116.
- Padmavathy TV, et al. Design of I-shaped dual C-slotted rectangular microstrip patch antenna (I-DCSRMPA) for breast cancer tumor detection. Cluster Computing(2018): 1-9.
- Youssef A, El-Telbany M, Zekry A. The role of artificial intelligence in photo-voltaic systems design and control: a review. Renew Sustain Energy Rev 78 (2017): 72–79
- Gad HH, Haikal AY, Ali HA. New design of the PV panel control system using FPGA-based MPSoC. Sol Energy 146 (2017): 243–256.
- Chekired F, Larbes C, Mellit A. Comparative study between two intelligent MPPT-controllers implemented on FPGA: application for photovoltaic systems. Int J Sustain Energy 33 (2014): 483–499.
- Lughofer E, Sayed-Mouchaweh M. Autonomous data stream clustering implementing split-and-merge concepts: towards a plug-and-play approach. Inf Sci 304 (2015): 54–79.
- de la Cruz-Alejo J, R. Antonio-Méndez and M Salazar-Pereyra. Fuzzy logic control on FPGA for two axes solar tracking. Neural Computing and Applications 31 (2019): 2469-2483.
- de Jesus Rubio J, Ochoa G, Meda JA, Rangel VI, Pacheco J. Acquisition system and analytic fuzzy model of a manufactured wind turbine. IEEE Lat Am Trans 13 (2015): 3879–3884.
- Finite Element Analysis for Temperature Distribution of Breast, Quin-yuan Lin, Shu-sen Xie, Shu-qiang Chen, Zheng Ye., IEEE/ICME 2007.
- EYK Ng, LN Ung, FC Ng, LSJ Sim. Statistical Analysis of Healhy and Malignant Breast Thermography. Journal of Medical Engineering and Technology 25 (2001): 253-263.
- Ng EY-K, Fok SC, Peh YC, Ng FC, Sim LSJ. Computerized detection of breast cáncer with artificial intelligence and thermograms. Journal of Medical Engineering & Technology 41 (2002): 152-157.
- Rockinger, Michael, and Eric Jondeau. Entropy densities with an application to autoregressive conditional skewness and kurtosis. Journal of Econometrics106 (2002): 119-142.