Biomechanical Analysis of Femur with THA and RHA implants using CT-Image Based Finite Element Method
Article Information
Mitsugu Todo1,*, Kosei Fukuoka2
1Research Institute for Applied Mechanics, Kyushu University, kasuga-koen, Kasuga, Fukuoka, Japan
2Interdisciplinary Graduate School of Engineering Sciences, Kyushu University, kasuga-koen, Kasuga, Fukuoka, Japan
*Corresponding Author: Mitsugu Todo, Associate Professor, Research institute for Applied Mechanics, Kyushu University 6-1 Kasuga-koen, Kasuga, Fukuoka, Japan
Received: 3 April 2020; Accepted: 13 April 2020; Published: 16 April 2020
Citation: Mitsugu Todo, Kosei Fukuoka. Biomechanical Analysis of Femur with THA and RHA implants using CT-Image Based Finite Element Method. Journal of Orthopaedics and Sports Medicine 2 (2020): 89-107.
Share at FacebookAbstract
The research demonstrates a novel three-dimensional finite element analysis to analyze biomechanical changes in a femur with two different type of hip prosthesis. The method used principal stress projections to determine trabeculae trajectories in the femur. Visual comparisons of the projections of the femurs show areas of cortical and cancellous changes due to changes in tensile and compressive stresses, revealing areas of stress shielding. The method also included a bone remodeling algorithm to simulate bone adaptation. In the analysis, a patient-specific femur model with inhomogeneous material properties was created from CT images. Maximum load during walking was simulated with realistic muscle forces, and stress projections of the femur model were compared to trabecular trajectories of a real femur for validation. Bone remodeling was also simulated to investigate changes in projections over time. High correlation was found between the principal stress projections of the computational model and trabeculae trajectories of a real femur. Changes in projections were evident for implant models, suggesting stress shielding and bone remodeling. The analysis provides an effective method for planning implants that are ideal for patients and for designing future implants that preserves the biomechanics of the femur to maintain its physiology.
Keywords
Biomechanics; Finite element analysis; Total hip arthroplasty; Bone remodeling
Hip arthroplasty articles Hip arthroplasty Research articles Hip arthroplasty review articles Hip arthroplasty PubMed articles Hip arthroplasty PubMed Central articles Hip arthroplasty 2023 articles Hip arthroplasty 2024 articles Hip arthroplasty Scopus articles Hip arthroplasty impact factor journals Hip arthroplasty Scopus journals Hip arthroplasty PubMed journals Hip arthroplasty medical journals Hip arthroplasty free journals Hip arthroplasty best journals Hip arthroplasty top journals Hip arthroplasty free medical journals Hip arthroplasty famous journals Hip arthroplasty Google Scholar indexed journals Osteoarthritis articles Osteoarthritis Research articles Osteoarthritis review articles Osteoarthritis PubMed articles Osteoarthritis PubMed Central articles Osteoarthritis 2023 articles Osteoarthritis 2024 articles Osteoarthritis Scopus articles Osteoarthritis impact factor journals Osteoarthritis Scopus journals Osteoarthritis PubMed journals Osteoarthritis medical journals Osteoarthritis free journals Osteoarthritis best journals Osteoarthritis top journals Osteoarthritis free medical journals Osteoarthritis famous journals Osteoarthritis Google Scholar indexed journals Avascular necrosis articles Avascular necrosis Research articles Avascular necrosis review articles Avascular necrosis PubMed articles Avascular necrosis PubMed Central articles Avascular necrosis 2023 articles Avascular necrosis 2024 articles Avascular necrosis Scopus articles Avascular necrosis impact factor journals Avascular necrosis Scopus journals Avascular necrosis PubMed journals Avascular necrosis medical journals Avascular necrosis free journals Avascular necrosis best journals Avascular necrosis top journals Avascular necrosis free medical journals Avascular necrosis famous journals Avascular necrosis Google Scholar indexed journals Total hip arthroplasty articles Total hip arthroplasty Research articles Total hip arthroplasty review articles Total hip arthroplasty PubMed articles Total hip arthroplasty PubMed Central articles Total hip arthroplasty 2023 articles Total hip arthroplasty 2024 articles Total hip arthroplasty Scopus articles Total hip arthroplasty impact factor journals Total hip arthroplasty Scopus journals Total hip arthroplasty PubMed journals Total hip arthroplasty medical journals Total hip arthroplasty free journals Total hip arthroplasty best journals Total hip arthroplasty top journals Total hip arthroplasty free medical journals Total hip arthroplasty famous journals Total hip arthroplasty Google Scholar indexed journals Acetabulum articles Acetabulum Research articles Acetabulum review articles Acetabulum PubMed articles Acetabulum PubMed Central articles Acetabulum 2023 articles Acetabulum 2024 articles Acetabulum Scopus articles Acetabulum impact factor journals Acetabulum Scopus journals Acetabulum PubMed journals Acetabulum medical journals Acetabulum free journals Acetabulum best journals Acetabulum top journals Acetabulum free medical journals Acetabulum famous journals Acetabulum Google Scholar indexed journals Hemispherical cup articles Hemispherical cup Research articles Hemispherical cup review articles Hemispherical cup PubMed articles Hemispherical cup PubMed Central articles Hemispherical cup 2023 articles Hemispherical cup 2024 articles Hemispherical cup Scopus articles Hemispherical cup impact factor journals Hemispherical cup Scopus journals Hemispherical cup PubMed journals Hemispherical cup medical journals Hemispherical cup free journals Hemispherical cup best journals Hemispherical cup top journals Hemispherical cup free medical journals Hemispherical cup famous journals Hemispherical cup Google Scholar indexed journals Resurfacing hip arthoplasty articles Resurfacing hip arthoplasty Research articles Resurfacing hip arthoplasty review articles Resurfacing hip arthoplasty PubMed articles Resurfacing hip arthoplasty PubMed Central articles Resurfacing hip arthoplasty 2023 articles Resurfacing hip arthoplasty 2024 articles Resurfacing hip arthoplasty Scopus articles Resurfacing hip arthoplasty impact factor journals Resurfacing hip arthoplasty Scopus journals Resurfacing hip arthoplasty PubMed journals Resurfacing hip arthoplasty medical journals Resurfacing hip arthoplasty free journals Resurfacing hip arthoplasty best journals Resurfacing hip arthoplasty top journals Resurfacing hip arthoplasty free medical journals Resurfacing hip arthoplasty famous journals Resurfacing hip arthoplasty Google Scholar indexed journals Bone cement articles Bone cement Research articles Bone cement review articles Bone cement PubMed articles Bone cement PubMed Central articles Bone cement 2023 articles Bone cement 2024 articles Bone cement Scopus articles Bone cement impact factor journals Bone cement Scopus journals Bone cement PubMed journals Bone cement medical journals Bone cement free journals Bone cement best journals Bone cement top journals Bone cement free medical journals Bone cement famous journals Bone cement Google Scholar indexed journals Osteolysis articles Osteolysis Research articles Osteolysis review articles Osteolysis PubMed articles Osteolysis PubMed Central articles Osteolysis 2023 articles Osteolysis 2024 articles Osteolysis Scopus articles Osteolysis impact factor journals Osteolysis Scopus journals Osteolysis PubMed journals Osteolysis medical journals Osteolysis free journals Osteolysis best journals Osteolysis top journals Osteolysis free medical journals Osteolysis famous journals Osteolysis Google Scholar indexed journals Biomechanical risks articles Biomechanical risks Research articles Biomechanical risks review articles Biomechanical risks PubMed articles Biomechanical risks PubMed Central articles Biomechanical risks 2023 articles Biomechanical risks 2024 articles Biomechanical risks Scopus articles Biomechanical risks impact factor journals Biomechanical risks Scopus journals Biomechanical risks PubMed journals Biomechanical risks medical journals Biomechanical risks free journals Biomechanical risks best journals Biomechanical risks top journals Biomechanical risks free medical journals Biomechanical risks famous journals Biomechanical risks Google Scholar indexed journals Osteopenia articles Osteopenia Research articles Osteopenia review articles Osteopenia PubMed articles Osteopenia PubMed Central articles Osteopenia 2023 articles Osteopenia 2024 articles Osteopenia Scopus articles Osteopenia impact factor journals Osteopenia Scopus journals Osteopenia PubMed journals Osteopenia medical journals Osteopenia free journals Osteopenia best journals Osteopenia top journals Osteopenia free medical journals Osteopenia famous journals Osteopenia Google Scholar indexed journals Trajectorial Theory articles Trajectorial Theory Research articles Trajectorial Theory review articles Trajectorial Theory PubMed articles Trajectorial Theory PubMed Central articles Trajectorial Theory 2023 articles Trajectorial Theory 2024 articles Trajectorial Theory Scopus articles Trajectorial Theory impact factor journals Trajectorial Theory Scopus journals Trajectorial Theory PubMed journals Trajectorial Theory medical journals Trajectorial Theory free journals Trajectorial Theory best journals Trajectorial Theory top journals Trajectorial Theory free medical journals Trajectorial Theory famous journals Trajectorial Theory Google Scholar indexed journals Computed tomography articles Computed tomography Research articles Computed tomography review articles Computed tomography PubMed articles Computed tomography PubMed Central articles Computed tomography 2023 articles Computed tomography 2024 articles Computed tomography Scopus articles Computed tomography impact factor journals Computed tomography Scopus journals Computed tomography PubMed journals Computed tomography medical journals Computed tomography free journals Computed tomography best journals Computed tomography top journals Computed tomography free medical journals Computed tomography famous journals Computed tomography Google Scholar indexed journals Femur articles Femur Research articles Femur review articles Femur PubMed articles Femur PubMed Central articles Femur 2023 articles Femur 2024 articles Femur Scopus articles Femur impact factor journals Femur Scopus journals Femur PubMed journals Femur medical journals Femur free journals Femur best journals Femur top journals Femur free medical journals Femur famous journals Femur Google Scholar indexed journals Calcar femorale articles Calcar femorale Research articles Calcar femorale review articles Calcar femorale PubMed articles Calcar femorale PubMed Central articles Calcar femorale 2023 articles Calcar femorale 2024 articles Calcar femorale Scopus articles Calcar femorale impact factor journals Calcar femorale Scopus journals Calcar femorale PubMed journals Calcar femorale medical journals Calcar femorale free journals Calcar femorale best journals Calcar femorale top journals Calcar femorale free medical journals Calcar femorale famous journals Calcar femorale Google Scholar indexed journals
Article Details
Introduction
Hip arthroplasty is a type of joint replacement surgery that has been the standard treatment for patients with osteoarthritis, avascular necrosis, and/or fracture within the hip joint. The two main surgical procedures for hip arthroplasty are the total hip arthroplasty (THA) and the resurfacing hip arthoplasty (RHA), with the former procedure replacing both the acetabulum and the femoral head and the latter only replacing the acetabulum. THA, the more common of the two procedures, requires three components: a stem and a spherical head that replaces the femoral head, and a hemispherical cup with an inner liner to replace the acetabulum. Stems with an interchangeable neck component, known as modular implants, are also available for hip joints with excessive anteversion or retroversion. RHA also utilizes a hemispherical cup for the acetabulum, except the femoral component is a cap that covers, or “resurfaces”, the femoral head.
While fundamental concept of hip arthroplasty has changed little since its appearance in medicine, the implants have experienced numerous changes in terms of material and design [1]. During the early stages of development, the THA implant had a metal-on-metal (MOM) bearing combination. All components were made cobalt-chrome alloy and bone cement was used to fixate the implant to the bone. The implant head was also similar in size as the anatomical head, giving the hip a natural physiological range of motion (ROM). When it was revealed that MOM produced high frictional torque, metal-on-polymer became the popular bearing combination choice. It soon became evident that debris from the plastic liner due to volumetric wear led to osteolysis and causing the implant to loosen. Thus, the implant head size was reduced to decrease the wear, which also decreased the ROM of the hip, limiting the patient’s mobility. The next fifty years saw the introduction of two more bearing combinations (ceramic-on-polymer and ceramic-on-ceramic), though much of the implant designs and the small head size remained unchanged. This drawback led to the development of the RHA implant, and re-introduced the use of MOM. Conservation of bone stock and increased ROM made RHA implants popular for younger, more active patients [2]. Presently, hip implants are available in all bearing combinations and in various shapes and sizes. THA implants with large head size are also becoming popular, as researches have shown that with larger head sizes, lubrication regime changes from boundary lubrication to fluid-film lubrication [3]. New researches in materials have also led to bearings having very low frictional coefficients. In addition, porous coatings around the stem have led to the development of cementless implants, providing stronger bone fixation than using bone cement.
However, there are still risks to hip arthroplasty and thousands of revision surgery is conducted each year. The main indications for surgery that concerns the implant are aseptic loosening, dislocation, and the wear of acetabular component [4]. The main risk factors are can be categorized as being mechanical, biological, or biomechanical. Mechanical risk factors include incorrect determination of implant size, position, and orientation. As mentioned earlier, using a smaller implant head size decreases the ROM of the hip and increases the risk of the implant impinging with the cup, leading to dislocation [5, 6]. Biological risk factors are derived from improper choice of implant type. With implants using bearing combinations of a polymer, the wear particles are associated with osteolysis, causing aseptic loosening of the implant. With MOM implants, the release of metal ions has been linked to metallosis. In addition, the size of head has been known to coincide with volumetric wear, with increasing head size leading to greater wear [7]. Both mechanical and biological risks have been heavily discussed in literature, and with proper clinical assessment and pre-surgical planning, the occurrence of these risks could be minimized. However, biomechanical risk factors are based on the remodeling of the bone, or the biological response due to mechanical change. Stress shielding is one factor in which the body load is shifted from the femur to the implant, causing osteopenia [8-12]. Such condition can cause aseptic loosening due to instability in fixation, or cause sudden fatal damage to the femur, such as fracture. In order to clinically assess biomechanical risks from an engineering perspective, researchers have focused on the bone adaptation theory [13-19]. The first bone adaptation theory, known as “Wolff’s Law” suggests that the bone adapts to changes in stress and tries to minimize load. Wolff also illustrated his version of principal stress projections and postulated the “Trajectorial Theory”, in which he noted that cancellous bone architecture is formed of a network of perpendicular intersections [20]. While Wolff’s Law has remained as the philosophy of bone remodeling, the Trajectory Theory has been dismissed by modern research, as it has been found that the cancellous architecture is non-orthogonal, and its orientation is governed clearly by loading [21].
Finite element analysis (FEA) has frequently been used to simulate physiology of the femur, using patient-specific three-dimensional models made from computed tomography (CT) scan and inhomogeneous material properties calculated from the Hounsfield unit (HU) of the CT scan [22]. The use of FEA has allowed researchers to examine stresses and strains and to conduct risk assessments. Recently, the push for realism has introduced the use of telemetry devices to determine hip contact force in real time. Combining the data with musculoskeletal modeling has allowed researchers to mimic realistic physiological loading conditions [23-26]. Numerical and computational bone adaptation theory has also been suggested, following three basic concepts: alteration in bone architecture due to mechanical stimulus, calculation of updated material property, and calculation of new stress and strain fields from updated material properties [27-31]. Computationally derived principal stress projections have also been evaluated with trabeculae structure of the femur with success [32, 33].
Despite of the advancements in materials and designs, hip implants continue to cause complications. The National Joint Registy (NJR) for England and Wales, which has a large population and high rates of coverage, have recently revealed that the revision rate for MOM implants, specifically RHA implants, was much higher than other bearing combinations [34, 35]. The findings have led to government health agencies in England and the United States to release alerts on the use of particular hip implants. Furthermore, within the past 10 years, major implant companies have recalled their implants. While researches concerning implant design have been conducted, most have been based on minimizing mechanical and biological risks. Patient-specific implants have also been simulated; however, the advantages have been minor compared to the cost and time to manufacture such implants [36-40]. Furthermore, long-term safety has not been addressed, which is a key factor for femur and implant survival, as well as the quality of life for the patient. Ideally, there should be minimal differences between the biomechanics of an intact femur and that of a femur with implant. Any alterations in loading will affect the stress and strain distribution, which will cause respective changes in the trabecular structure and henceforth the bone density. Thus, the primary design criteria of an implant must be based on minimizing biomechanical risks, followed by the minimization of mechanical and biological risks. In order to assess the effectiveness and safety of the implant design, it is necessary to first replicate the biomechanics of the femur, test under realistic physiological conditions, followed by bone remodeling simulation to predict long-term outcome. To the best of our knowledge, the combination of the three works has not yet been reported in literature. The goal of this research was to investigate whether FEA and computational simulations of human physiology can be utilized to assess implant designs and formulate design criteria for future implant design. The objectives of this study were to realistically simulate the physiological condition of the femur, to investigate the effects of an implant in the femur, and to simulate long-term effects.
2. Finite Element Modeling
2.1 3D models
CT scans (512 x 512, 1 mm slices) from a male 54yo patient were used to make an intact bone model. MECHANICAL FINDER 6.1 (Research Center of Computational Mechanics Inc., Japan) (MF) was used to trace region of interest (ROI) around the outer cortical region on the scans to obtain the anatomical structure of the left femur. The ROIs were then stacked and the gaps between the CT scans were automatically conjoined by the software to create a femur volume. The volume was surface meshed (unstructured linear triangular mesh) using ANSYS ICEM CFD v13 (ANSYS Inc., USA). Rapidform XOR3 (INUS Technology Inc., USA) was used to smooth the meshed model, and FEMAP 10.1.1 (Siemens PLM Software, USA) was used for all editing made on the meshed model. The final volume was remeshed (unstructured linear tetrahedral mesh) in MF as shown in (Figure 1). CAD models of THA and RHA implant were directly imported into MF. RHA model consisted of a 48 mm ? cap, identical to the size of the patient’s femoral head as shown in (Figure 2). A bone cement model of two-millimeter thickness was created for the RHA implant model and fitted between the implant and the femoral head. THA implant consisted of a 156 mm length stem and a 34 mm ? head. All models were meshed with linear unstructured tetrahedral mesh. The intact bone models were then grinded so that those implants were inserted into the bone models as shown in (Figure 3).
Figure 1: Intact bone model.

Figure 2: THA and HRA implants.
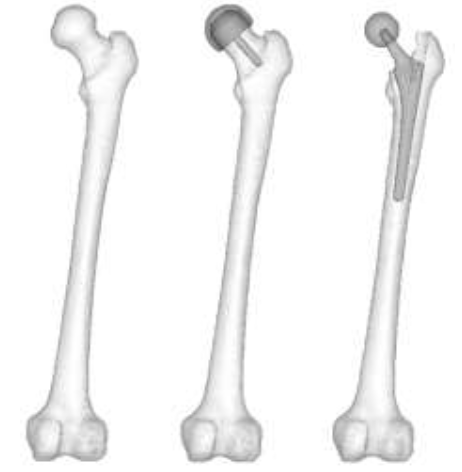
Figure 3: Intact bone, RHA, and THA model.
2.2 Material properties
Material properties of the femur were derived from the ash density extracted from the HU of the CT scans using the following formula:

The Young’s modulus and the yield stresses were calculated from the ash density as proposed by Keyak et. al [41]. The Poisson’s ratio was set to 0.3. For the THA implant, Ti-6Al-4V alloy was assigned to the stem and alumina to the head for a ceramic-on-polymer bearing condition. For the RHA implant, Co-Cr-Mo alloy was assigned to the cap. Material properties of poly (methyl methacrylate) (PMMA) was set to bone cement. The Young’s moduli of Ti-6Al-4V, Co-Cr-Mo, alumina and PMMA were set to be 114, 230, 370, and 2.65GPa, respectively. The Poisson’s ratios of them were 0.34, 0.30, 0.32, and 0.42, respectively.
2.3 Boundary conditions
Simplified maximum walking contact forces determined by Heller et. al were applied to the models [42]. The forces used in the analysis are listed in (Table 1). Each % body weight (BW) was configured with the patient’s BW. Modifications were made on the locations of the origin and insertion of the muscle, as well as the distributions, for a realistic anatomical representation.
|
Type of load |
Forces (N) |
|
Intersegmental resultant |
483.19 |
|
Abductor |
632.30 |
|
Tensor fascia late, proximal |
115.20 |
|
Tensor fascia latae, distal |
115.38 |
|
Vastus lateralis |
574.64 |
Table1: Physiological loading during walking.
Simplified abductor muscles were expanded to include gluteus medius, gluteus minimus, and gluteus maximum to the correct anatomical position and distribution as shown in (Figure 4). The porous coating on the upper half of the implant was assumed to be fully bonded with the bone (Figure 5). Non-porous areas were assumed to have a friction coefficient of 0.2. In the case of RHA, contact options between the implant and bone cement, and between the bone cement and bone was considered, set at 0.3 and 0.5, respectively. Fixed constraint was applied to the distal femur.
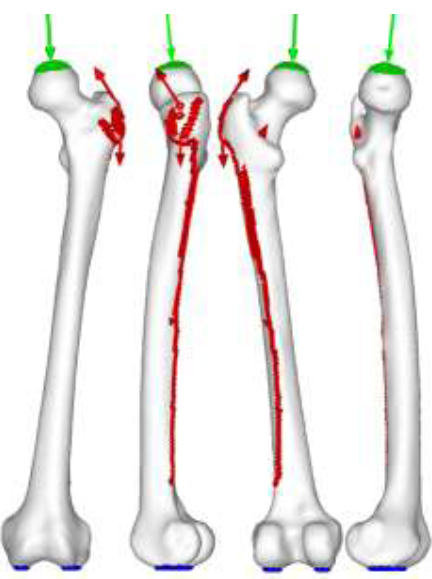
Figure 4: Walking contact force.
Intersegmental resultant = green | muscle = red | constraint = blue.
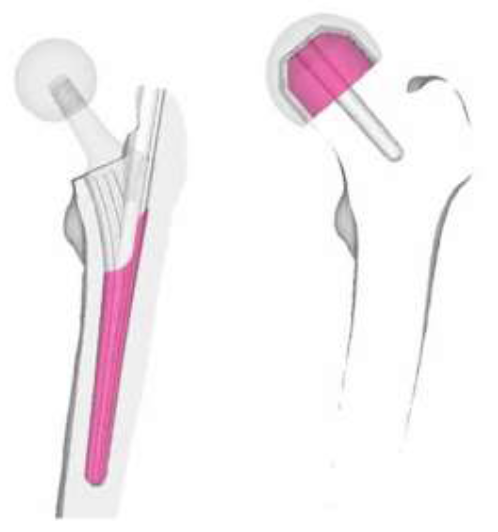
Figure 5: Contact option applied to implants.
2.4 Bone adaptation algorithm
Bone adaptation algorithm proposed by Huiskes et. al was used in this experiment [43]. In the theoretical formulation, the rate of remodeling as the change of Young’s modulus, dE/dt, was correlated with the strain energy density, U, as follows:
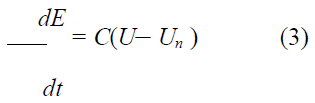
Where C and Un are the remodeling constant and the site specific homeostatic equilibrium strain energy density, respectively. In the present analysis, C and Un were set at 1.2×105 and 0.011MJ/m3, respectively.
3. Results
3.1 Principal stress projections of intact model
Preliminary principal stress projections predicted by FEA were compared to the CT scan of the patient as shown in (Figure 6). In the CT scan, a distinct hypodense structure can be seen from the top of the femoral head tracing downwards to the calcar femorale of the femur. This is represented as the minimum principal stress (red) on the FEA result. The epiphyseal line can also be seen in the CT scan, near the center of the femoral head. This is traceable by the maximum principal stress (blue). With the FEA result, it is also possible to view the five trabeculae groups: principal tensile and compressive group (dashed), secondary tensile and compressive group (dotted), and the greater trochanter group (Figure c). When the groups are superimposed, the patterns reveal Ward’s Triangle (W), the area with the minimum bone density. In addition, the projections indicate that the trabeculae do not form a network of perpendicular intersections, as postulated in the Trajectory Theory.
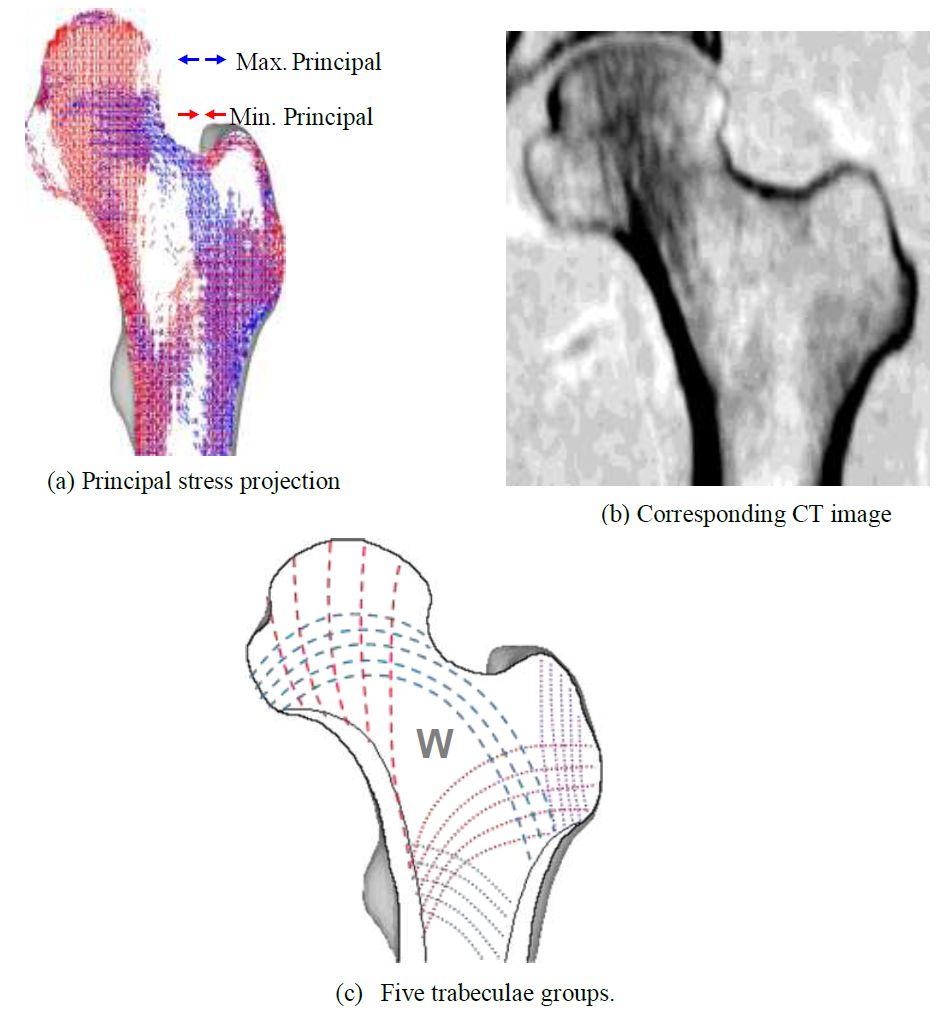
Figure 6: Coronal principal stress projection, patient CT image and five trabecular groups.
(Figure 7) shows the principal stress projection in the transverse plane. It is possible to see both the epiphyseal line and the calcar femoral, that are very similar to the real anatomical structure of femur. These similarities between the FEA results and the real femoral structure indicate that 3D FEA can realistically predict trabeculae structure due to the stress projections being determined from material properties and not the symmetry. The intact bone was attested to be an appropriate control for the experiment.
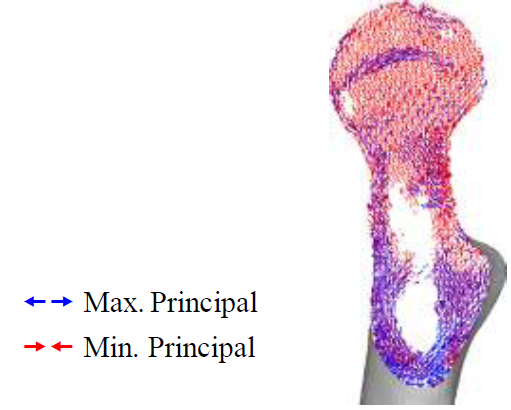
Figure 7: Principal stress projection in transverse plane.
The preliminary HRA projections show similar characteristics to the intact bone model as shown in (Figure 8). Much of the trabeculae groups remained, with little change in the greater trochanter region. However, the diaphysis show decrease in stress projections. It is also possible to see a collection of stress projections near the tip of the stem, despite the stem superimposing Ward’s triangle. While the overall trabecular structure may have become sparse with the insertion of the implant, much of the trabecular characteristics are maintained.
None of the trabeculae groups remain in the THA model due to the absence of the femoral head. While the intact bone model indicates pure compressive loading along the medial region, the calcar femorale region shows tensile loading. Contrastingly, the lateral region shows increase in minimum principal stresses, indicating high compressive loading and densification of the trabeculae near the middle of the stem. Like the RHA model, the greater trochanter region does not significantly change regarding projection.

Figure 7: Principal stress projection in transverse plane.
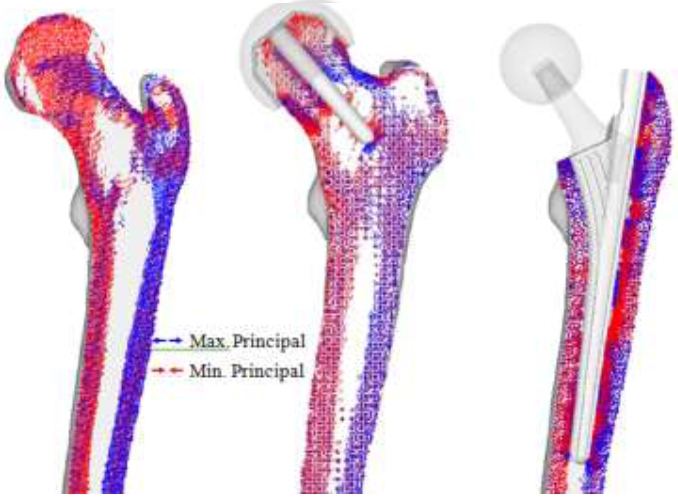
Figure 8: Preliminary principal stress projection (intact bone, THA, RHA).
To assess the post-operative safety of the implant, the equivalent stress distribution of each model was investigated and compared to the intact bone model. Drucker-Prager yield criterion was chosen as bone is a brittle material and the compressive strength is higher than the tensile strength [44, 45]. In addition, excluding the RHA and THA models, implant designs with high stress and wide distribution were assumed to be deficient and were omitted from further experimentation. The equivalent stress for RHA shows almost identical distribution as the intact bone model as shown in (Figure 9). THA model equivalent stress distribution reveal that the proximal lateral section experiences high stress, while the distal lateral section experiences low stress. However, the stress increases around the implant tip. Proximal medial region, around the porous coating of the implant, also experiences high stress, although it appears to decrease distally.
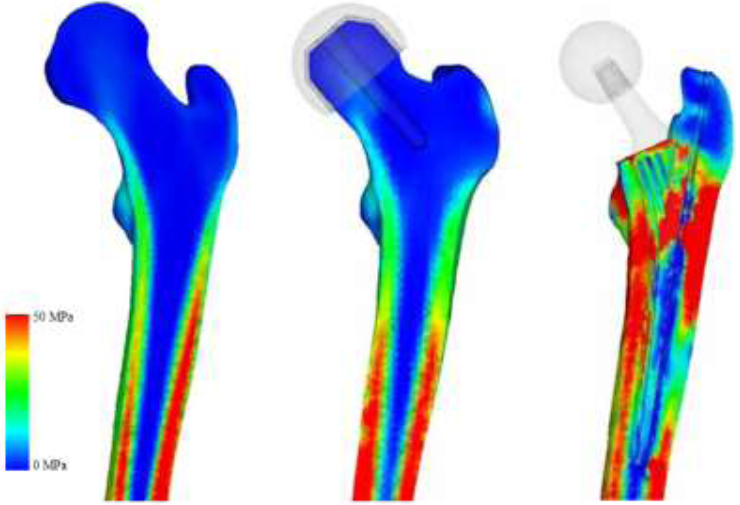
Figure 9: Drucker-Prager equivalent stress (intact bone, THA, RHA).
Preliminary inspection is important to inspect the changes in the physiology of post-operative femur, but so far, only the mechanical aspects (i.e. results based on material properties) have been considered. In order to assess post-operative conditions and long-term outcomes, bone remodeling simulation is required. Bone remodeling was conducted on the THA and RHA implants. The intact bone model was not simulated for bone remodeling due to the assumption that, excluding critical health conditions, there is no significant change in bone structure for the given time that implanted femurs reach steady state (i.e., no further bone remodeling occurs). Thus, all implant models were remodeled until steady state was reached. The results for the RHA implant are shown in (Figure 10). Significant changes occur in the femoral head, as the disappearance of trabeculae groups causes formations of an unnatural trabeculae group. At t1, the disappearance of primary compressive group at the top half of the femoral head can be seen, and whole of the bottom half being directed from the implant stem. A collection of projections can also be seen near the calcar femoral. Much of the primary tensile group has disappeared, as well as both secondary groups.
As seen in the preliminary stress projection, a collection of projections exists around the tip of the stem. At t2, all trabeculae groups have disappeared, and a formation of a new compressive group, projecting from the stem towards the greater trochanter can be seen. As the modeling enters steady state, the femoral head is absent of distinct projections; however, region around the calcar femorale and the stem tip contains stress projections, and both medial and lateral stress projections have remained.
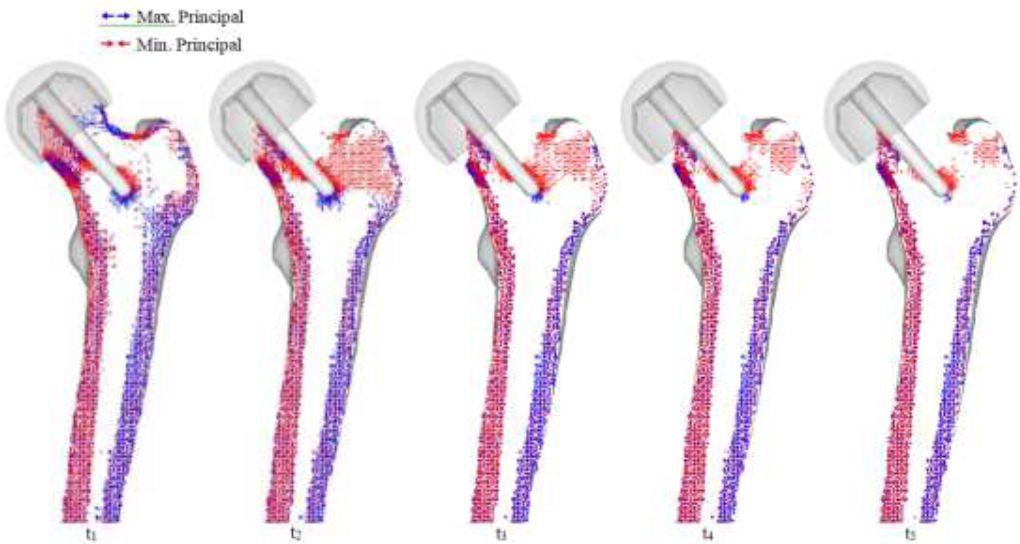
Figure 10: RHA bone remodeling with principal stress projections.
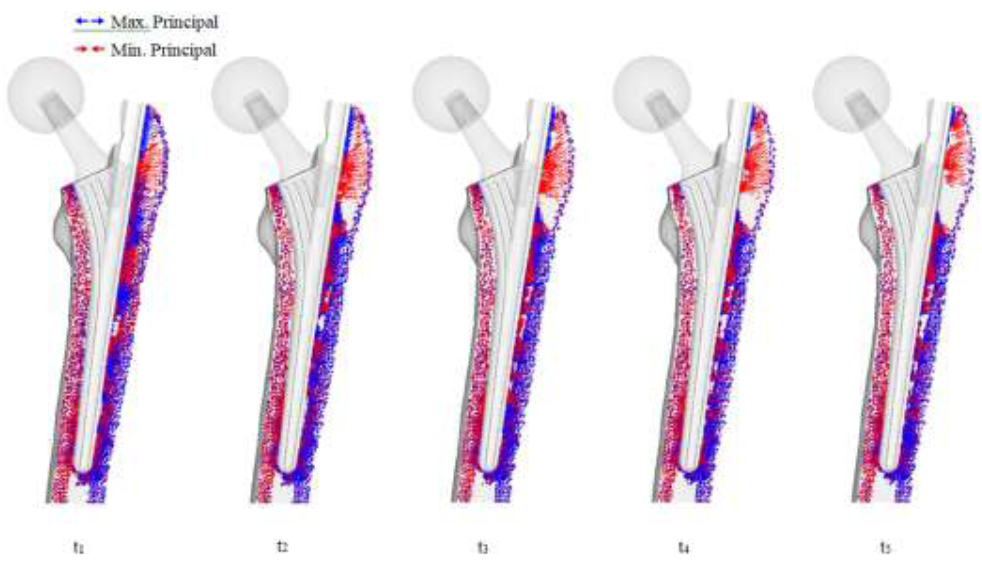
Figure 11: THA bone remodeling with principal stress projections.
The significant change with the THA implant model is the restoration of the medial and lateral projections, as well as the projections at the calcar femorale, which has changed back to compressive projections as shown in (Figure 11). Collections of projections still remain along the surface of the implant and stem tip, and continues until the remodeling reaches steady state. A clear area without projections also appears beneath the greater trochanter.
3.5 Bone mineral density
Bone mineral density (BMD) was analyzed to link projections to trabeculae structure and the results are shown in (Figure 12). For implant models, this was calculated at t5, or the steady state stage. BMD of the intact bone was directly derived from the CT scans. From the BMD, the quality of the bone stock can be determined, which reflects on the strength of the bone as well as areas which may become the focal point for risks. Areas of high BMD correlates to high stress and/or stress shielding, and areas of low BMD reveals weakening of the bone and potential risk triggers. Like the stress projections, the BMD distribution is very similar to the intact bone. The diaphysis has maintained BMD on both the medial and lateral regions. However, there is a significant decrease in density in the femoral head. The distributions show that BMD is low around the porous coating, and high around the uncoated region. The stem tip also shows increased BMD. The shorter length model has a larger distribution in which density has increased. The stem tip on the larger headed implant, on the other hand, does not show signs of increased BMD.
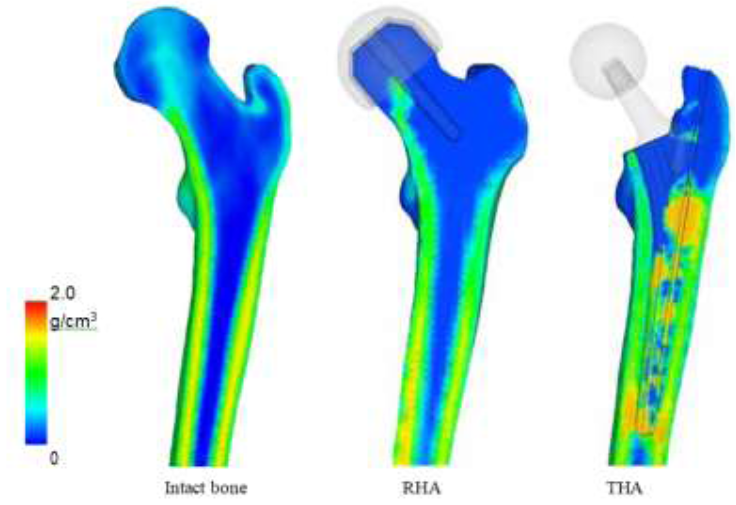
Figure 12: Bone mineral density after bone remodeling.
4. Discussion
The preliminary principal stress projections showed that RHA implants are superior in design as the trabecular groups were maintained and the diaphysis was under the correct loading. This indicated that upon initial loading, RHA implants could maintain the same trabeculae structure the femur had before arthroplasty. The Drucker-Prager equivalent stress distributions also had similar results. The distribution of the RHA implant was comparable to that of the intact bone. At first glance, it appears that the RHA is inferior to the THA implant design, but in reality this is not the case. Inspecting the biological aspects, bone remodeling revealed a contradicting yet realistic result. Due to the RHA implant supporting much of the load, stress projections gradually diminished, indicating increase in cancellous region in the femoral head. Furthermore, due to the location of the stem, there are indications of bone densification in Ward’s triangle, an area known to have low strength, consisting only of cancellous structure. Newly formed trabeculae structures fanning from the stem to the greater trochanter also indicates unnatural trabeculae growth. BMD results also indicate a decrease in density in the femoral neck. While the diaphysis remains strong (stronger than the THA models), the weakening of the femoral neck is inevitable. It clearly shows that the upper region of the femoral head has minimum support. From these findings it is easy to understand why femoral neck fracture is common for RHA implants. THA implants showed significant changes in the trabeculae structure in the preliminary experiment which was able to maintain the characteristics of the diaphysis. When the Drrucker-Prager equivalent stress was inspected, THA models revealed extremely high stress areas around the proximal region. Again, the distributions of the larger head-sized implant were akin to the intact bone model.
While bone remodeling simulation has revealed that the diaphysis returns to its original state, the lateral proximal region, below the greater trochanter, and the tip of the implant stem, remains to be an issue. This finding was also reflected with the BMD analysis, where increased bone density was found in identical locations. Such characteristics where two highly densified areas separated by low density region could lead to peri-prosthetic fracture. In all cases, the implant closely matched the results of the intact bone model. The main simulation limitation is the use of linear tetrahedral elements. For FEA, quadratic tetrahedral elements, or, if computationally possible, linear hexahedral or quadratic hexahedral should be used, as linear tetrahedral elements have been known to be too stiff due to lower degrees of freedom, which could produce unrealistic results. Furthermore, recent bone adaptation algorithms have included the effect of stimulus on a cellular level, specifically the effect of mechanical stimulus on the osteocyte. This leads to the importance of dynamic loading, not static loading, as used in this experiment. Such use of algorithms would further realistically simulate bone adaptation. In addition, modeling real muscle tissue and not musculoskeletal loading will further amplify realistic femur physiology. In addition, the main experimental limitation is the small sample size, for only a single patient’s CT scan was used throughout the experiment. While increasing the number of patient data will reveal trends, the result will always be patient-specific. It should be noted that that true validation for implant designs is derived from case studies, where the subject’s age, sex, and gender, as well as the implant size, material, and bearing combination play an important role. Clinical studies must also be considered, where the patient’s health, the condition of the femur, and the skill and experience of the surgeon are important factors. Furthermore, the number of such studies will also reflect the validity of research. Despite of this, the research has closely achieved clinical results with engineering methodology. It has also shown that mechanical assessment is not enough to effectively evaluate the implant. Biomechanical assessment must be conducted to fully establish the safety of a design.
5. Conclusions
A novel process to realistically simulate long-term biomechanics of femur with implants has been proposed. FEA has provided to be an integral tool to realistically model the biomechanics of the femur, with the use of realistic physiological loading conditions. Computational modeling of bone adaptation has also predicted the long-term physiological outcome of a femur with implant, and conducting risk assessments have revealed possible fracture areas due to long-term remodeling. Using this process, implant designers can investigate the femur physiology of design, and determine long-term effects by performing bone adaptation and risk assessment, before the design enters production. Medical doctors can also benefit from this process during pre-operative planning stage. An ideal implant can be chosen purely from the patient’s femur’s biomechanics, and long-term assessments can estimate when post-operative follow-up should be performed before serious damages occur.
References
- Gomez PF, Morcuende JA, Early attempts at hip arthroplasty- 700s TO 1950s.The Iowa Orthopaedic Journal 25 (2005): 25-29.
- Shrader MW, Bhowmik-Stoker M, Jacofsky MC, et al. Gait and stair function in total and resurfacing hip arthroplasty: a pilot study. Clinical orthopaedics and related research 467 (2009): 1476-1484.
- Dowson D, Hardaker C, Flett M, et al. A hip joint simulator study of the performance of metal-on-metal joints. The Journal of Arthroplasty 19 (2004): 124-130.
- Porter M, Tucker K, Beaumont R, et al. National Joint Rgistry for England and Wales 9th Annual Report (2012).
- Malik A, Maheshwari A, Dorr LD. Impingement with total hip replacement. The Journal of bone and joint surgery. American volume 89 (2007): 1832-1842.
- Kelley SS, Lachiewicz PF, Hickman JM, et al. Relationship of femoral head and acetabular size to the prevalence of dislocation. Clinical orthopaedics and related research 355 (1998): 163-170.
- Lavigne M, Ganapathi M, Mottard S, et al. Range of motion of large head total hip arthroplasty is greater than 28 mm total hip arthroplasty or hip resurfacing. Clinical biomechanics (Bristol, Avon) 26 (2011): 267-273.
- Joshi MG, Advani SG, Miller F, et al. Analysis of a femoral hip prosthesis designed to reduce stress shielding. Journal of biomechanics 33 (2000): 1655-1662.
- Abdullah AH, Asri MNM, Alias MS et al. Finite Element Analysis of Cemented Hip Arthroplasty : Influence of Stem Tapers, in Proceedings of the International MultiConference of Engineers and Computer Scientists 3 (2010).
- Behrens B, Wirth CJ, Windhagen H, et al. Numerical investigations of stress shielding in total hip prostheses. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine 222 (2008): 593-600.
- Abdullah AH, Nor MAM, Saman AM. Stress and Strain Distribution in Cemented Total Hip Arthroplasty for Walking Load Case in 2009 International Conference on Computer Technology and Development (2009): 260-263.
- Ridzwan MIZ, Shuib S, Hassan AY, et al. Ridzwan, MIZ - Problem of Stress Shielding and Improvement to the Hip Implant DesignA Review. Journal of Medical Sciences 7 (2007): 460-467.
- Kowalczyk P. Simulation of orthotropic microstructure remodelling of cancellous Journal of biomechanics 43 (2010): 563-569.
- Garcia JM, Doblare M, Cegonino J. Bone remodelling simulation : a tool for implant design. Computational Materials Science 25 (2002): 100-114.
- Herrera A, Panisello JJ, Ibarz E, et al. Long-term study of bone remodelling after femoral stem: a comparison between dexa and finite element simulation. Journal of biomechanics 40 (2007): 3615-3625.
- Scannell PT, Prendergast PJ. Cortical and interfacial bone changes around a non-cemented hip implant: simulations using a combined strain/damage remodelling algorithm. Medical engineering and physics 31 (2009): 477-488.
- Belinha J, Natal Jorge RM, Dinis LMJS. Bone tissue remodelling analysis considering a radial point interpolator meshless method. Engineering Analysis with Boundary Elements 36 (2012): 1660-1670.
- Kerner J, Huiskes R, van Lenthe GH, et al. Correlation between pre-operative periprosthetic bone density and post-operative bone loss in THA can be explained by strain-adaptive remodelling. Journal of biomechanics 32 (1999): 695-703.
- Waide V, Cristofolini L, Stolk J, et al. Experimental investigation of bone remodelling using composite femurs. Clinical Biomechanics 18 (2003): 523-536.
- Skedros JG, a Brand R. Biographical sketch: Georg Hermann von Meyer (1815-1892). Clinical orthopaedics and related research 469 (2011): 3072-3076.
- Skedros JG, Baucom SL. Mathematical analysis of trabecular trajectories in apparent trajectorial structures: the unfortunate historical emphasis on the human proximal femur. Journal of theoretical biology 244 (2007): 15-45.
- Keyak JH, a Rossi S, a Jones K, et al. Prediction of femoral fracture load using automated finite element modeling. Journal of biomechanics 31 (1998): 125-133.
- Bergmann G, Graichen F, a Rohlmann, et al. Realistic loads for testing hip implants. Bio-medical materials and engineering 20 (2010): 65-75.
- Bergmann G, Deuretzbacher G, Heller M, et al. Hip contact forces and gait patterns from routine activities. Journal of biomechanics 34 (2001): 859-871.
- Simoes JA, Vaz MA, Blatcher S, et al. Influence of head constraint and muscle forces on the strain distribution within the intact femur. Medical engineering and physics 24 (2002): 243.
- Bitsakos C, Kerner J, Fisher I, et al. The effect of muscle loading on the simulation of bone remodelling in the proximal femur. Journal of biomechanics 38 (2005): 133-139.
- Fyhrie D, Schaffler M. The adaptation of bone apparent density to applied Journal of biomechanics 28 (1995): 135-146.
- Weinans H, Huiskes R, Grootenboer HJ. Effects of material properties of femoral hip components on bone remodeling. Journal of orthopaedic research 10 (1992): 845-853.
- Turner CH, Anne V, Pidaparti RM. A uniform strain criterion for trabecular bone adaptation: do continuum-level strain gradients drive adaptation? Journal of biomechanics 30 (1997): 555-563.
- Mullender M, van Rietbergen B, Rüegsegger P, et al. Effect of mechanical set point of bone cells on mechanical control of trabecular bone architecture. Bone 22 (1998): 125-131.
- Huiskes R, Weinans H, Grootenboer HJ. Adaptive bone-remodeling theory applied to prosthetic-design analysis. Journal of … 20 (1987): 1135-1150.
- San Antonio T, Ciaccia M, Müller-Karger C, et al. Orientation of orthotropic material properties in a femur FE model: a method based on the principal stresses directions. Medical engineering and physics 34 (2012): 914-919.
- Dick C, Georgii J, Burgkart R, et al. Stress tensor field visualization for implant planning in orthopedics. IEEE transactions on visualization and computer graphics 15 (2009): 1399-1406.
- Smith AJ, Dieppe P, Vernon K, et al. Failure rates of stemmed metal-on-metal hip replacements: analysis of data from the National Joint Registry of England and Wales. Lancet 379 (2012): 1199-1204.
- Smith AJ, Dieppe P, Howard PW, et al. Failure rates of metal-on-metal hip resurfacings: analysis of data from the National Joint Registry for England and Wales. Lancet 380 (2012): 1759-1766.
- Chang PB, Robie BH, Bartel DL. Preclinical cost analysis of orthopaedic implants: a custom versus standard cementless femoral component for revision total hip arthroplasty. Journal of biomechanics 32 (1999): 1309-1318.
- Baleani M, Viceconti M, Muccini R, et al. Endurance verification of custom-made hip prostheses. International Journal of Fatigue 22 (2000): 865-871.
- Bert JM. Custom total hip arthroplasty. The Journal of arthroplasty 11 (1996): 905-915.
- Götze C, Steens W, Vieth V, et al. Primary stability in cementless femoral stems: custom-made versus conventional femoral prosthesis. Clinical biomechanics (Bristol, Avon) 17 (2002): 267-273.
- Kawate K, Ohneda Y, Ohmura T, et al. Computed tomography-based custom-made stem for dysplastic hips in Japanese patients. The Journal of arthroplasty 24 (2009): 65-70.
- Keyak, a Rossi S, a Jones K, et al. Prediction of femoral fracture load using automated finite element modeling. Journal of Biomechanics 31 (1998): 125-133.
- Heller M, Bergmann G, Kassi JP. Determination of muscle loading at the hip joint for use in pre-clinical Journal of Biomechanics 38 (2005): 1155-1163.
- Huiskes R, Weinans H, Grootenboer HJ. Adaptive bone-remodeling theory applied to prosthetic-design analysis. Journal of Biomechanics 20 (1987): 113 5-1150.
- Bessho M, Ohnishi I, Matsuyama J, et al. Prediction of strength and strain of the proximal femur by a CT-based finite element method. Journal of biomechanics 40 (2007): 1745-1753.
- Wakao N, Harada A, Matsui Y, et al. The effect of impact direction on the fracture load of osteoporotic proximal femurs. Medical engineering and physics 31 (2009): 1134–1139.
