A Stochastic View of Comorbidity in Speech Disorders
Article Information
Moura TRS*
Campus Salinopolis, Universidade Federal do Para, Salinopolis, PA, Brazil
*Corresponding Author: Dr. Moura TRS, Campus Salinopolis, Universidade Federal do Para, Salinopolis, PA, 68721-000, Brazil
Received: 04 March 2019; Accepted: 27 March 2019; Published: 05 April 2019
Citation: Moura TRS. A Stochastic View of Comorbidity in Speech Disorders. Journal of Psychiatry and Psychiatric Disorders 3 (2019): 067-079.
Share at FacebookAbstract
We used discrete random walks for the analysis of two chronic conditions that may be present simultaneously in a patient. We analyzed the comorbidity between two symptoms referring to the pathological repetition of speech: palilalia and echolalia. We used memory walks with coupled memory with probability f. The probability f quantifies the mutual interaction between pairs of random walkers. We perform measures that quantify two characteristics of the walks; one of the local nature, the fractal dimension (D) and another of a global nature, the exponent of Hust (H). We found that typical measures of D are related to less severe degrees of palilalia and echolalia, followed by variations smaller than H. The H measures show that the regime is superdiffusive and there is no transition between diffusion regimes. In the region of comorbidity, the diffusive regimes do not exhibit quantitative values of H of ERW. We find curves for which the symptoms of palilalia and echolalia do not vary. That is, certain changes in the environment, quantified by the feedback parameter (p) and the probability of interaction (f); do not cause variations in the degree of severity of the two types of pathological speech repetition that were studied.
Keywords
Palilalia, Echolalia, Coupling, Non-Markovian processes
Palilalia articles Palilalia Research articles Palilalia review articles Palilalia PubMed articles Palilalia PubMed Central articles Palilalia 2023 articles Palilalia 2024 articles Palilalia Scopus articles Palilalia impact factor journals Palilalia Scopus journals Palilalia PubMed journals Palilalia medical journals Palilalia free journals Palilalia best journals Palilalia top journals Palilalia free medical journals Palilalia famous journals Palilalia Google Scholar indexed journals Echolalia articles Echolalia Research articles Echolalia review articles Echolalia PubMed articles Echolalia PubMed Central articles Echolalia 2023 articles Echolalia 2024 articles Echolalia Scopus articles Echolalia impact factor journals Echolalia Scopus journals Echolalia PubMed journals Echolalia medical journals Echolalia free journals Echolalia best journals Echolalia top journals Echolalia free medical journals Echolalia famous journals Echolalia Google Scholar indexed journals Coupling articles Coupling Research articles Coupling review articles Coupling PubMed articles Coupling PubMed Central articles Coupling 2023 articles Coupling 2024 articles Coupling Scopus articles Coupling impact factor journals Coupling Scopus journals Coupling PubMed journals Coupling medical journals Coupling free journals Coupling best journals Coupling top journals Coupling free medical journals Coupling famous journals Coupling Google Scholar indexed journals Non-Markovian processes articles Non-Markovian processes Research articles Non-Markovian processes review articles Non-Markovian processes PubMed articles Non-Markovian processes PubMed Central articles Non-Markovian processes 2023 articles Non-Markovian processes 2024 articles Non-Markovian processes Scopus articles Non-Markovian processes impact factor journals Non-Markovian processes Scopus journals Non-Markovian processes PubMed journals Non-Markovian processes medical journals Non-Markovian processes free journals Non-Markovian processes best journals Non-Markovian processes top journals Non-Markovian processes free medical journals Non-Markovian processes famous journals Non-Markovian processes Google Scholar indexed journals Invasive developmental disorders articles Invasive developmental disorders Research articles Invasive developmental disorders review articles Invasive developmental disorders PubMed articles Invasive developmental disorders PubMed Central articles Invasive developmental disorders 2023 articles Invasive developmental disorders 2024 articles Invasive developmental disorders Scopus articles Invasive developmental disorders impact factor journals Invasive developmental disorders Scopus journals Invasive developmental disorders PubMed journals Invasive developmental disorders medical journals Invasive developmental disorders free journals Invasive developmental disorders best journals Invasive developmental disorders top journals Invasive developmental disorders free medical journals Invasive developmental disorders famous journals Invasive developmental disorders Google Scholar indexed journals autism spectrum disorder articles autism spectrum disorder Research articles autism spectrum disorder review articles autism spectrum disorder PubMed articles autism spectrum disorder PubMed Central articles autism spectrum disorder 2023 articles autism spectrum disorder 2024 articles autism spectrum disorder Scopus articles autism spectrum disorder impact factor journals autism spectrum disorder Scopus journals autism spectrum disorder PubMed journals autism spectrum disorder medical journals autism spectrum disorder free journals autism spectrum disorder best journals autism spectrum disorder top journals autism spectrum disorder free medical journals autism spectrum disorder famous journals autism spectrum disorder Google Scholar indexed journals neurodevelopmental disorder articles neurodevelopmental disorder Research articles neurodevelopmental disorder review articles neurodevelopmental disorder PubMed articles neurodevelopmental disorder PubMed Central articles neurodevelopmental disorder 2023 articles neurodevelopmental disorder 2024 articles neurodevelopmental disorder Scopus articles neurodevelopmental disorder impact factor journals neurodevelopmental disorder Scopus journals neurodevelopmental disorder PubMed journals neurodevelopmental disorder medical journals neurodevelopmental disorder free journals neurodevelopmental disorder best journals neurodevelopmental disorder top journals neurodevelopmental disorder free medical journals neurodevelopmental disorder famous journals neurodevelopmental disorder Google Scholar indexed journals idiosyncratic phrases articles idiosyncratic phrases Research articles idiosyncratic phrases review articles idiosyncratic phrases PubMed articles idiosyncratic phrases PubMed Central articles idiosyncratic phrases 2023 articles idiosyncratic phrases 2024 articles idiosyncratic phrases Scopus articles idiosyncratic phrases impact factor journals idiosyncratic phrases Scopus journals idiosyncratic phrases PubMed journals idiosyncratic phrases medical journals idiosyncratic phrases free journals idiosyncratic phrases best journals idiosyncratic phrases top journals idiosyncratic phrases free medical journals idiosyncratic phrases famous journals idiosyncratic phrases Google Scholar indexed journals pathological speech repetition articles pathological speech repetition Research articles pathological speech repetition review articles pathological speech repetition PubMed articles pathological speech repetition PubMed Central articles pathological speech repetition 2023 articles pathological speech repetition 2024 articles pathological speech repetition Scopus articles pathological speech repetition impact factor journals pathological speech repetition Scopus journals pathological speech repetition PubMed journals pathological speech repetition medical journals pathological speech repetition free journals pathological speech repetition best journals pathological speech repetition top journals pathological speech repetition free medical journals pathological speech repetition famous journals pathological speech repetition Google Scholar indexed journals neurocognitive disorders articles neurocognitive disorders Research articles neurocognitive disorders review articles neurocognitive disorders PubMed articles neurocognitive disorders PubMed Central articles neurocognitive disorders 2023 articles neurocognitive disorders 2024 articles neurocognitive disorders Scopus articles neurocognitive disorders impact factor journals neurocognitive disorders Scopus journals neurocognitive disorders PubMed journals neurocognitive disorders medical journals neurocognitive disorders free journals neurocognitive disorders best journals neurocognitive disorders top journals neurocognitive disorders free medical journals neurocognitive disorders famous journals neurocognitive disorders Google Scholar indexed journals
Article Details
1. Introduction
Developmental disorders are classified as specific and invasive. Specific disorder is characterized by developmental delays in a specific area or specific areas, whereas invasive disorder has deficiencies in basic functions in multiple contexts that includes socialization and communication. Invasive developmental disorders (TID) are part of the autism spectrum disorder group. Autism spectrum disorder affects more than 1% of children in the United States [1]. It is classifed as a non-degenerative neurodevelopmental disorder, accompanied by symptoms such as delay in verbal and non-verbal communication; resistance to routine change; restricted and persistence interests in relation to an activity, topic, object, speech, idiosyncratic phrases, etc., abnormalities in eye contact and body expression; difficulties in initiating and maintaining social relations. Symptoms may vary from mild to moderate or severe [2]. The possibility of developing similar physical models to assist in the understanding of mental disorders, which may enable the development of new diagnostic tools. Based on the symptoms and diagnostic criteria, we present a model that uses discrete random walks as a possible diagnostic tool for two types of pathological speech repetition: echolalia and palilalia. The Diagnostic and Statistical Manual of Mental Disorders (DSM5) describes a significant spectrum of mental disorders: neurodevelopmental disorders and neurocognitive disorders. Some of these disorders may have one or more symptoms in common. Neurodevelopmental disorders, for example, such as Tourette’s syndrome, Asperger’s syndrome, autistic spectrum disorders (ASD), persistent vocal tic disorder, transient vocal tic disorder, psychotic disorder due to another medical condition, catatonia associated with another mental disorder, etc. These disorders can be accompanied by pathological, parody and seemingly meaningless (echoing) repetition of a word or phrase. This pathology can be divided into two subtypes: echolalia and palilalia. Echolalia is defined as the pathological, parody and apparently meaningless (echoing) repetition of a word or phrase that has just been spoken by another person. Palilalia is the repetition or imitation of an echo made by a person in relation to words just uttered by that same person (self echolalia). Numerous studies are aimed at examining the causes, correlations between neurodevelopmental disorders and the pathological repetition of discourse, providing manuals of treatments and specialized training for health professionals and society in general [3-9].
In the Diagnostic and Statistical Manual of Mental Disorders (DSM5), which describes neatly a broad spectrum of neurodevelopmental disorders and neurocognitive disorders, symptomatic aspects, diagnostic criteria, risk factors, prognosis, differential diagnosis, etc [2]. Based on these symptoms, we propose a physical model to quantify the pathological repetition of words or phrases. We present the pathological repetition of speech in the perspective of stochastic processes. The choice of discrete random walks allows us to make an analogy between these symptoms and the diffusive process. In this analogy the constructed model allows to associate the echolalia and the palilalia with measures typical of physical observables of the random walks. To make the analysis of autistic behavior, by analogy with the diffusive system formed by random walkers, we need to define a system that serves as the standard for terms of comparison. To this end, we have defined the ERW model as the standard. The reasons for our school are: (a) it has well-known diffusive regimes, (b) the propagator is known, (c) has a well-known analytical solution, and (d) is a widely used model for building other models of non-Markovian random walks [10-18].
The relevant aspects of the Schutz and Trimper model, their main characteristics and diffusion regimes are described below. This model describes discrete random walks with uniform memory profile, which considers a discrete random walk of history relevant to the next walker’s decisions. At every instant of time t the information is recovered in an equiprobable way. Therefore, the probability that an action taken in the past is 1/t, to t being the current time. The random walk is recorded at all times, this aspect attributes to the process a non-Markovian characteristic. The stochastic dynamics of the process occur in the following way: the walker starts in time t0 in a position x0, at each moment of time the walker walks one step to the right or step to the left, with probability p e (1 ? p), respectively. For this process, the stochastic evolution equation is given by the equation:

for the time t+1. The variable σt+1 assumes the value +1 when the walker walks one step to the right and -1 when the walker walks one step to the left. The memory consists of a set of random variables σt' for the time t' < t that the hiker can recover. This process occurs as follows:
(a) at time t+1 a number t' of the set 1, 2, …, t is chosen randomly with uniform probability 1/t.
(b) σt+1 is determined stochastically by obeying the following relations, σt+1 = σt' with probability p e σt+1 = -σt' with probability 1- p.
The first step at time t=1, occurs according to the following dynamics: the walker is in position X0 and moves to the right with probability q or to the left with probability 1-q, that is, σ1=+1 with probability q and σ1=-1 with probability 1-q. The stochastic evolution equation is:

The parameter p is the probability of the walker repeating an action from the past in a time t'. When (p>1/2) the walker presents a persistent behavior, this is characterized by the repetition of past actions. For (p<1/2) the walker takes an action contrary to the action that was selected, presenting an anti-persistent behavior. For the value of (p=1/2) the random walk is Markovian. In the boundary regions of (p=0) and (p=1) two extreme behaviors arise. The maximum persistent behavior occurs in (p=0) the maximum of the persistent behavior, while in (p=1) the maximum persistent behavior occurs, in the latter case the movement is ballistic, characterized by the typical value of the Hurst exponent (H=1). The first moment of the position is

With β=2q?1, α=2p?1 and Γ is the gamma function. The α and β parameters are defined in the range [?1, 1]. Using the α parameter we can characterize the random walk as persistent for α > 0 and anti-persistent for α < 0.
The second moment of the position is given by
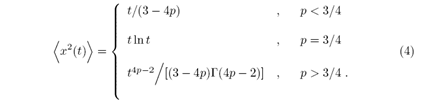
The diffusive behavior changes with the probability values p, when (p <3/4) the second moment depends linearly on t and the diffusion is regular (H=1/2), to (p >3/4) diffusion is characterized as superdiffusive, for the intermediate case (p=3/4) the second moment is described by a logarithmic function cite ERW. Additional information about the ERW model, such as probability distribution, the study of its limits, etc. can be verified in cite ERW, BB, GH2.
2. The Model
Our model consists of a pair of random walkers with memory coupled with probability f. The first random walker is the ERW model, which is defined as healthy behavior. The second, which presents the behavior invariant to changes, represents the autistic. The decisions of each walker are influenced by the decisions of the other (or by his own history) with probability f (1?f). When walkers are not influenced by the microscopic decisions of the other, with probability (1-f), this phenomenon is associated with the palilalia symptom. As the probability (f) increases, each set of random walkers becomes influenced by the story of the other. We associate this behavior with the echolalia symptom. The higher the probabilities of interaction (not interaction) the greater the typical values of f (1-f) the higher the degrees of echolalia (palilalia). The first walker we call “Professor” and the second of “Student”. When the Professor and student do not learn from each other, each student makes decisions based only on his / her own history, representing the maximum of palilalia (associated with the most severe degree of palilalia). As f grows interest by the parody repetition of the speech of the other is less restricted, there is mutual repetition of speech. The maximum (minimum) of mutual influence occurs when f=1 (f=0). At the outset of microscopic dynamics, Student imitates (“learns”) the Professor’s decisions with probability f. In like manner the Professor learns (does not learn) with the Student, that is, the decisions of the Student are known by the Professor with probability f.
For this problem, however, we note that the interaction is bilateral. We will show the construction of our model, which led us to the reasoning above. Through the use of random walks with coupled memory; the Professor can learn (not learn) from Student’s actions with probability fP (1-P), likewise, Student can learn (not learn) with Professor probability fA (1-A). In this way, as the two random walkers may have an impact on the microscopic dynamics of each other.
Only for reasons of order, let us call the ERW model of Professor and the other of Student. Our model describes the interaction between the two discrete random walkers (Professor and Student). We define the Professor as the ERW model, whose microscopic dynamics has already been described previously. The Student begins his movement in the position Y0, in time t0=0, at each instant of time the random walker walks one step to the right, remaining persistently in the same decision to every instant of time. The quantification of this behavior is performed by the stochastic equation:

where ?t+1 is a random variable, assuming the values of σt' when the random walker behaves like the ERW model. The Student accepts the decisions of the ERW model with probability fA and rejects with probability (1-fA), when the walker makes decisions based on his own history. The memory is formed by a set of random variables ?t' t' < t, which the walker remembers as follows:
(a) in time t + 1 a number t' of the set 1, 2, …, t is chosen in an equipotable manner 1/t.
(b) the variable ?t+1 is determined stochastically as ?t+1= ?t'.
The first step at time t=1, the walker is in the position Y0, accepting (rejecting) the ERW model with probability fA (1-fA), with the equation of stochastic evolution quantifying this process for all time:

Since the student accepts (rejects) Professor’s decisions with probability fA (1-fA), we note that the random variable ?t' can be rewritten as:
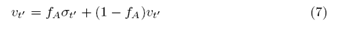
which allows us to rewrite the student’s stochastic equation as:
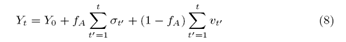
At the maximum of non-learning, fA=0, Student recalls actions only from his history, his stochastic equation is given by (6), another end, fA=1, when there is maximum interaction, the stochastic equation is written as:

therefore, less than the first step, Y0, the process is described by the ERW model. Similarly, for the Professor, to encompass the ability to learn, we make the Professor susceptible to the actions of the Student. The Professor’s dynamics, too, will be influenced by Student’s decisions with probability fP and not influenced with probability 1- fP. The stochastic equation (2) is modified by the following transformation:
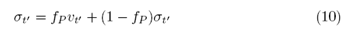
resulting in the stochastic equation, which describes the learning of the ERW model with respect to the Student.
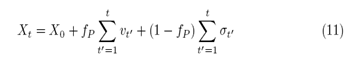
At the point, fP=0, which quantifies the minimum of interaction, the random walker behaves like the ERW model, while fP=1 quantifies the Professor’s maximum learning probability relative to the actions of the Student. For the maximum interaction, fP=1, the stochastic equation takes the following form

being ?t' the stochastic variable that represents the student’s microscopic decisions. We can consider two cases for the probabilities of interaction between random walkers. The first case is the symmetric, when the probability of interaction of the two walkers is equal (fP=fA), and the second case is non-symmetric, when (fP ≠ fA). Let us address, in this work, the symmetric case (fP=fA). We set our model under these conditions. The maximum (minimum) coupling between Professor and Student will occur for the quantitative probability values equal to fP=fA=0 (fP=fA =1) which correspond to the minimum (maximum) of interaction, respectively. Therefore, we can vary a single probability value by calling fP=fA =f, we rewrite the equations (8) and (11) respectively as
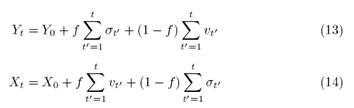
In the case of minimal interaction, f=0, the models retrieve their ordinary results, without mutual interaction, with the stochastic equations (6) and (2) for Student and for the ERW model, respectively. To quantify the measures of the coupling result, we consider the resulting vector in two-dimensional space

For our two-dimensional random walk case Xt and Yt are the stochastic variables of associated walkers, for example, axes x and y respectively. The random walkers interact according to the variations of the probability of interaction f, which quantifies the coupling between the random walkers. The equation (15) combines the characteristics of the two sets of walkers for the cases of palilalia (f=0) and echolalia (f=1).
We measure two physical quantities of interest; the fractal dimension D, which measures is the measure of the local roughness; the Hurst H exponent, which measures long-range persistence. The Hurst exponent (H) classifies the different diffusion regimes in random walks [22]. The variance spreads non-linearly with time σ2 =< r2 > + < r >2α t2H. The local properties (D) and the global property H, are related according to the equation

where ? the spatial dimension in Euclidean space [23].
3. Results
Our model is formed by discrete random walks with coupled memory. The variance is characterized by the faster growth of the second moment when we compare to the first moment of the position, therefore, the variance can be approximated by the ratio < r2 >~ t2H. The means are estimated for our finite length walks consisting of 104 hiking pairs of size 107. We perform the estimates of two gratings which provide us with global and local property information of the system, quantified here by the measures of the Hurst exponent and fractal dimension, which are obtained through the relations < r2 >~ t2H and D=3-H, respectively.
In the Figure 1, we display measures of the fractal dimension. The measures are presented as a function of the feedback parameter p and the coupling probability f. In the color panel, lighter shades are associated with smaller fractal dimension measurements, while larger values of D are related to darker color tones. The panel displays a spectrum of fractal dimension measurements in the range 1.9 ≤ D ≤ 2.4. We observe that objects in Euclidean space have entire dimensions, but dimensions related to fractal geometry objects can be fractioned. For example, for a fractal dimension value (D=1.9), the object has a dimension between the dimension of an object in one-dimensional Euclidean space (D=1) and a two-dimensional object (D=2). At the other end of the displayed values for the panel is the value (D=2.4), which is associated with an object with dimension between the dimension of a two-dimensional object (D=2) and a three-dimensional object (D=3).
Looking at the results of the Figure 1, we can perform two types of analysis, one varying f by keeping p fixed and another by changing p and keeping f fixed. Keeping f fixed and varying p, we observe that D decreases as p → 1. Typical values of D in this case are: for f=0.7 fixed, p=0.1 we have D ≈ 2.3391 and p=0.9 we get D ≈ 2.0454. To perform the analysis according to the second perspective, we traced the graph by keeping p fixed and varying f. We get p=0; f=0 the value of D ≈ 2, f=0.6 the value of D ≈ 2.377 and p=1 with D measuring approximately 2. Note that the function is concave and presents, according to our numerical results, a maximum spectrum when the probability interaction assumes values of f >≈ 0.6 for all p.
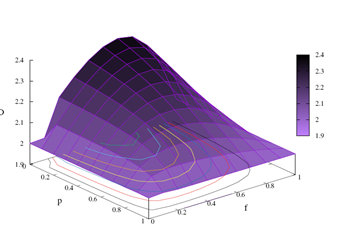
Figure 1: 3D diagram of the fractal dimension as a function of feedback parameter p and the probability of coupling f among random walkers. The color diagram was plotted to display a gradient between the purple and black colors. The display shows the intensity variation from purple to black. Typical measurements of the fractal dimension are displayed in the panel where the lowest intensity of purple is related to smaller measures of D, starting with the value D=1.9. Darker shades are associated with larger fractal dimension measurements, reaching their maximum value for D=2.4.
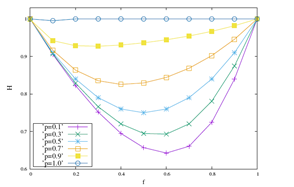
The results discussed above are reinforced when we look at the Figure 2. In it, measurements of the fractal dimension and Hurst’s exponent are displayed for values of p equal to 0.1, 0.3, 0.5, 0.7, 0.9 and 1 with the probability of coupling in the range 0 ≤ f ≤ 1. In the Figure 2 (a) the results of D show that D is a function concave with maximum in f >≈ 0.6, for any of the values of p. We note, maintaining fixed, that greater D variations are accompanied by lower values of p. The inverse of this behavior is shown in Figure 2 (b), where the function is convex. Maintaining f fixed lower variations of H are associated with higher values of p. Its minimum point occurs for f >≈ 0.6. Therefore, for larger values of p, smaller are the variations of the local physics observable D, which are accompanied by larger measurements of the global physics observable H.
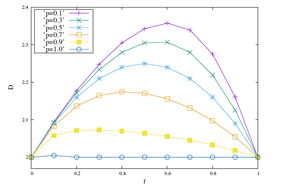
(a) Fractal dimension.
Figure 2: The behaviors of D and H are displayed as a function of the probability of interaction f e for ordinary values of p equal to 0.1, 0.3, 0.5, 0.7, 0.9 and 1.
(b) Hurst exponent.
Figure 2: The behaviors of D and H are displayed as a function of the probability of interaction f e for ordinary values of p equal to 0.1, 0.3, 0.5, 0.7, 0.9 and 1.
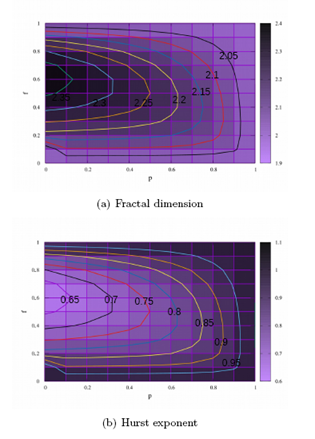
In the Figure 3 maps of D and H are displayed for the feedback and coupling parameters, respectively, in the ranges of 0 ≤ p ≤ 1 and 0 ≤ f ≤ 1. In Figure 3 (a) are highlighted curves with typical values of the fractal dimension equal to 2.05, 2.1, 2.15, 2.2, 2.25, 2.3 and 2.35. From the local point of view, to go through each of these curves the fractal dimension remains the same. Therefore, to traverse the curve with D=2.2 varying p and f, the measure of the roughness remains invariant. From the global point of view, in the Figure 3 (b), the values of the Hurst exponent are displayed. Curves for variations of H equal to 0.65, 0.7, 0.75, 0.8, 0.85 and 0.95 are highlighted. These curves show that for certain variations p and f, measurements of the observable physics H remain invariant.
(b) Hurst exponent.
Figure 3: Color maps are displayed for D and H. Each map has two extreme colors: purple and black. The maps display a gradient between these two colors. Typical measurements of D and H are smaller (larger) for lighter shades (dark). In the Figure 3 (a) the map of the fractal dimension is displayed and in the Figure 3 (b) the map of the Hurst exponent.
4. Discussion
According to [17], measures of the Hurst exponent greater than 1/2, for which the regime is over diffusive, are associated with degrees of autism. The higher the values of H the more severe is the degree of autism associated, when analyzed from the perspective of restricted interests. The higher the values of H, the greater the degree of restricted interests related to random walkers associated with the diffusive regimes.
Observing the Figure 1, the 3D diagram shows the most severe palilalia degree when f=0, random walkers exhibit typical values of D=2, which are associated with the ballistic diffusive regime characterized by quantitative values of Hurst’s exponent H=1. As f increases the values of D increase to values of p, for example, equal to 0.1 as can be seen in Figure 2 (a). Traversing the f axis, the values of D get their highest value in f >≈ 0.6, which decreases to values equal to D=2 to f=1. Lower D values are associated with a more severe degree of palilalia for the point f <≈ 0.6. At the most severe echolalia point f=1 we get the same value for the roughness measure D=2. In the point of palilalia (echolalia) f=0 (f=1) more severe the diffusive regime is ballistic H=1, accompanied by values typical of the fractal dimension equal to D=2. In the interval 0 < f < 1 between the extreme points, we have the simultaneous coexistence of palilalia and echolalia, causing this region implies in the region of comorbidity between these two symptoms. The point of least severity between these two symptoms occurs in f >≈ 0.6, where the fractal dimension has its highest value and the Hurst exponent shows its highest value, as can be seen in the Figure 2. Therefore, the point f <≈ 0.6 is the critical point of comorbidity between the symptoms of palilalia and echolalia.
In the Figure 3 the maps referring to the fractal dimension and Hurst’s exponent measurements are displayed. In each one of them are highlighted curves whose measures do not vary according to certain changes of f and p. In the Figure 3 (a) the curves of equal measure of D are shown, i.e. curves of equal roughness with ordinary values equal to 2.05, 2.1, 2.15, 2.2, 2.25, 2.3 and, 2.35, which do not vary for certain combinations of f and p. Similarly, in the Figure 3 (b), we highlight curves that have values for fixed H, all of which quantify the over diffusive regime, their values are 0.65, 0.7, 0.75, 0.8, 0.85, 0.9 and 0.95, curves for which the changes of f and p do not imply changes of H, i.e. are curves of equal diffusivity. As the measured values for D and H are presented for the interval 0 < f < 1, we therefore have the region of the simultaneous existence of palilalia and echolalia, i.e. the region of comorbidity of these symptoms. In this perspective, we note that the equal dimension curves D and of equal diffusivity are curves of equal comorbidity, for them the degrees of palilalia and echolalia do not change according to the variations of the feedback parameter and the coupling probability f.
5. Conclusions
The Diagnostic and Statistical Manual of Mental Disorders (DSM5) describes that some neurodevelopmental disorders may have common symptoms, such as Tourette’s syndrome, autistic spectrum disorders (ASD), persistent vocal tic disorder, transient vocal tic disorder, psychotic disorder due to another medical condition, among other disorders. One such symptom is pathological, parody and seemingly meaningless (echoing) repetition of a word or phrase, such as echolalia and palilalia. We used a discrete random walk model, which consists of pairs of random walkers with memory coupling. Minimum (maximum) coupling is associated with palilalia (echolalia) where random walkers do not imitate (mimic) the microscopic behavior of each other with probability f (1-f). We performed measures of the fractal dimension and the Hurst exponent, which quantify local properties and global property, respectively. We need that the more severe degrees of palilalia (f=0) and echolalia (f=1) are associated with values smaller than D and related to larger measures of H, when compared with measures in the region 0 < f < 1. For values of the coupling probability in the region 0 < f < 1, which is the region of comorbidity between palilalia and echolalia, the curves of the measurements of D (H) are concave (convex), for the parameter of feedback p fixed, with critical value in f >≈ 0:6. We find curves of equal comorbidity, which are curves for which the symptoms of palilalia and echolalia do not vary, according to certain variations of the feedback parameter and the probability of interaction. We hope that these results may contribute to a better understanding of echolalia and palilalia and the simultaneous existence of symptoms in patients with invasive developmental disorders.
References
- Baio J, Wiggins L, Christensen DL, et al. Prevalence of Autism Spectrum Disorder Among Children Aged 8 Years| Autism and Developmental Disabilities Monitoring Network, 11 Sites, United States, 2014. MMWR Surveillance Summaries 67 (2018): 1-23.
- Diagnostic and Statistical Manual of Mental Disorders: DSM5. (5th) (2013).
- Howlin P, Asgharian A. The diagnosis of autism and Asperger syndrome: findings from a survey of 770 families. Dev Med Child Neurol 41 (1999): 834-839.
- Johnson CP, Myers SM. Council on Children with Disabilities. Identification and evaluation of children with autism spectrum disorders. Pediatrics 120 (2007): 1183-1215.
- Mandell DS, Maytali MN, Zubritsky CD. Factors associated with age of diagnosis among children with autism spectrum disorder. Pediatrics 116 (2005): 1480-1486.
- Martinez-Pedraza F, Carter A. Autism spectrum disorders in young children. Child Adolesc Psychiatr Clin N Am 18 (2009): 645-663.
- Ozono S, Young GS, Steinfeld MB, et al. How early do parent concerns predict later autism diagnosis? Journal of Developmental Behavioral Pediatrics 30 (2009): 367-375.
- Pickles A, Simono E, Conti-Ramsden G, et al. Loss of language in early development of autism and specific language impairment. Journal of Child Psychology and Psychiatry 50 (2009): 843-852.
- Rogers SJ. Developmental regression in autism spectrum disorders. Ment Retard Dev Disabil Res Rev 10 (2004): 139-143.
- Schutz GM, Trimper S. Elephants can always remember: Exact long-range memory effects in a non-Markovian random walk. Phys Rev E 70 (2004).
- Cressoni JC, da Silva MAA, Viswanathan GM. Amnestically Induced Persistence in Random Walks. PRL 98 (2007).
- Felisberto ML, Passos FS, Ferreira AS, et al. Sudden onset of log-periodicity and superdiffusion in non-Markovian random walks with amnestically induced persistence: exact results. Eur Phys J B 72 (2009): 427.
- da Silva MAA, Viswanathan GM, Ferreira AS, et al. Spontaneous symmetry breaking in amnestically induced persistence. Phy Rev E 77 (2008).
- Cressoni JC, Viswanathan GM, Ferreira AS, et al. Alzheimer random walk model: Two previously overlooked diffusion regimes. Phy Rev E 86 (2012).
- Borges GM, Ferreira AS, da Silva MAA, et al. Superdiffusion in a non-Markovian random walk model with a Gaussian memory profile. Eur Phys J B 85 (2012): 310.
- Alves GA, de Araujo JM, Cressoni JC, et al. Superdiffusion driven by exponentially decaying memory. J Stat Mech (2014).
- Thiago RS Moura, Viswanathan GM, da Silva MAA, et al. Transient superdiffusion in random walks with a q-exponentially decaying memory profile. Physica A 453 (2016).
- Diniz RMB, Cressoni JC, da Silva MAA, et al. Narrow log-periodic modulations in non-Markovian in random walks. Phy Rev E 96 (2017).
- Baur E, Bertoin J. Elephant Random Walks and their connection to Pólya-type urns. Phys Rev E 94 (2016).
- da Silva MAA, Cressoni JC, Schutz GM, et al. Non-Gaussian propagator for elephant random walks. Phys Rev E 88 (2013).
- Moura TRS, Fulco UL, Albuquerque EL. A random walk model to evaluate autism. Physica A 492 (2018).
- Hurst HE, Black RP, Simaika YM. Long-Term Storage: An Experimental Study (Constable, London) (1965).
- Gneiting T, Schlather M. Stochastic Models That Separate Fractal Dimension and the Hurst Effect. SIAM Review 46 (2004).
